EIN
KOMPAKTER ÜBERBLICK

Nachfolgend werden Sensoren betrachtet, welche die dynamische Änderung geometrischer Größen bezogen auf die Zeit auswerten. Es geht also um Messgrößen wie die Geschwindigkeit bzw. deren zeitbezogene Änderung, die Beschleunigung. Wir gehen hierbei sowohl auf lineare wie auch Drehbewegungen ein. Abschließend werfen wir noch einen kurzen Blick auf inertiale Messsysteme sowie Satellitennavigationssysteme.
Drehzahlsensoren
Bei der Messung einer Drehzahl – definiert als Anzahl der Umdrehungen pro Zeiteinheit – dominieren zwei Sensorprinzipien: Beim Tachogenerator handelt es sich um einen meist als kleinen Wechselspannungsgenerator ausgeführten Sensor. Solche Anordnungen bestehen im einfachsten Fall aus einem umlaufenden Dauermagneten (Rotor), der in einer außenseitig angebrachten Spule (Stator) bei jedem Umlauf eine sinusförmige Welle erzeugt. Oftmals werden mehrere Dauermagnete mit entsprechenden Spulen kombiniert. Das Ausgangsspannungssignal eines Tachogenerators entspricht näherungsweise einem Sinussignal mit einer zur Drehzahl proportionalen Amplitude.
Bei der Drehzahlmessung über Impulsgeber werden an der Oberfläche des rotierenden Teils befindliche Strukturen abgetastet und als Impulssignal ausgegeben. Dies kann z.B. durch eine Art Zahnradstruktur passieren. Beim Vorbeilauf eines Zahns am Sensor wird ein vom Sensor erzeugtes magnetisches oder elektrisches Feld verändert, was entsprechend detektiert werden kann. Andere Varianten arbeiten beispielsweise mit einem Hall-Sensor oder dem Wirbelstromeffekt. Bei allen Impulsgebern müssen die Impulse extern über eine gewisse Messzeit gezählt werden.
Geschwindigkeitssensoren
Die Messung der Geschwindigkeit erfolgt im einfachsten Fall durch Ermitteln der Zeit t, die das Messobjekt zwischen zwei definierten Punkten zurücklegt, die einen Abstand s aufweisen. v lässt sich dann bekanntermaßen ermitteln gemäß
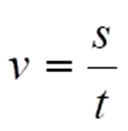
Das Verfahren wird häufig so implementiert, dass an den zwei definierten Punkten entsprechende Geber wie z.B. Lichtschranken das Passieren des Messobjekts anzeigen.
Ein weiteres Verfahren basiert auf der Bestimmung der Drehzahl eines rotierenden Körpers, woraus dann spezifisch zur Anordnung passend auf eine Lineargeschwindigkeit geschlossen werden kann. Am bekanntesten ist der Einsatz dieses Verfahrens beim Automobil, wo über den Reifenumfang auf die Fahrgeschwindigkeit geschlossen wird.
Bei einer radarbasierten Geschwindigkeitsmessung z.B. im Straßenverkehr erfolgt dies gemäß nachfolgendem Bild durch Aussenden eines Radarsignals vom Fahrbahnrand aus in Richtung des Fahrzeugs unter einem gewissen kleineren Winkel φ zur Fahrtrichtung des Fahrzeugs. Aufgrund der nie ganz ebenen Frontstruktur eines Fahrzeugs wird stets ein gewisser Signalanteil genau zum Radarsensor wieder zurück reflektiert, wo er dann empfangen wird. Das reflektierte Radarsignal erfährt eine Frequenzverschiebung fD nach dem Dopplereffekt und zwar zweimal: in Sende- wie auch in Empfangsrichtung. Mit der Wellenlänge λ ist diese
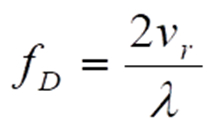
vr ist die radiale Geschwindigkeitskomponente des Fahrzeugs in Richtung Radarsensor. Sie berechnet sich aus der Fahrzeuggeschwindigkeit v gemäß
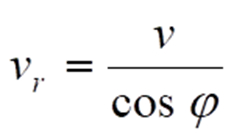
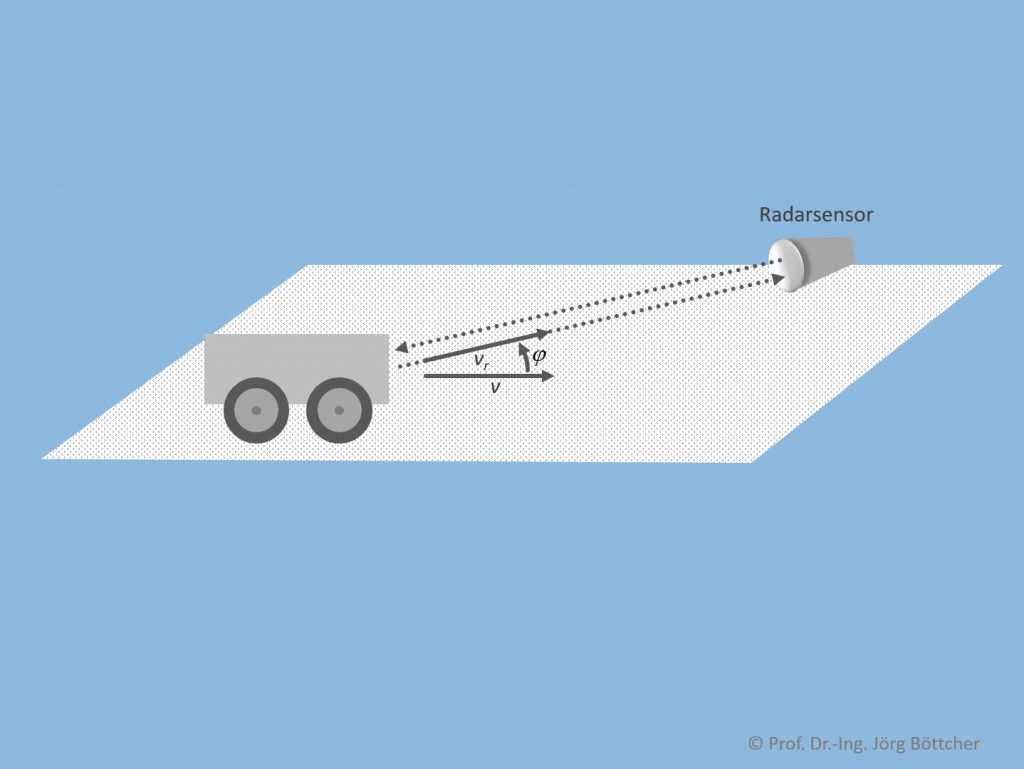
Dopplereffekt mit Radar
Bei vielen anspruchsvolleren Geschwindigkeitsmessanwendungen an bewegten Komponenten in der Industrie wird ein anderes, ebenfalls den Dopplereffekt ausnutzendes Verfahren angewandt (sog. Laser Surface Velocimeter): Zwei gegenüber der Mittelachse jeweils um einen kleinen Winkel versetzte Laserstrahlen werden senkrecht von oben auf einen Punkt an der Messoberfläche des sich fortbewegenden Objekts geleitet. Die Laserstrahlen sind in ihrer Lichtintensität sinusförmig moduliert. Im Projektionspunkt entsteht durch die Überlagerung ein Interferenzmuster. Bei Bewegung der Messoberfläche, die hierzu eine gewisse Struktur aufweisen muss, erfährt das zurück gestreute Laserlicht eine Frequenzverschiebung, die proportional der Messobjektgeschwindigkeit ist und entsprechend ausgewertet wird.
Drehratensensoren
Drehbewegungen laufen mit einer gewissen Winkelgeschwindigkeit ω in der Einheit rad/s, manchmal auch als °/s angegeben, ab. Sensoren zur Messung dieser werden meist als Drehratensensoren bezeichnet. Hat man eine sich drehende Welle o.ä. als Referenz, so kann man natürlich auch aus einer Drehzahlmessung n die Drehrate ω ableiten. Allerdings benötigt dies eine gewisse, entsprechend der erforderlichen Messgenauigkeit längere Messzeit.
Für schnelle Drehratenmessungen sind spezielle, i.d.R. auf MEMS-Basis (Micro Electro Mechanical System) gefertigte Drehratensensoren verfügbar. Gemäß unterem Bild sind auf dem Chip zwei Massen über eine Federstruktur miteinander verbunden. Sie werden über eine entsprechende Aktorik (z.B. elektromagnetisch) in eine Schwingung versetzt mit zugehöriger Momentangeschwindigkeit v(t). Bei Drehung um das Zentrum dieser Anordnung mit einer Drehrate ω wirken entsprechende Corioliskräfte FC auf die beiden Massen. Die Massen werden durch entsprechende Führungen am seitlichen Ausbrechen gehindert.
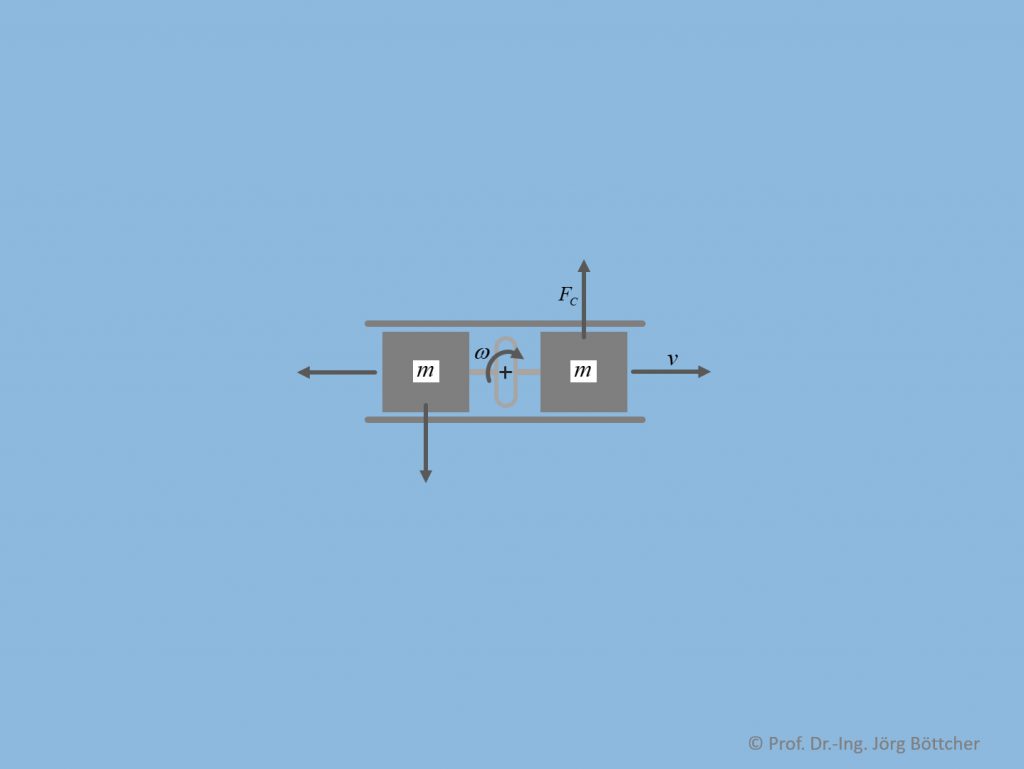
Technische Realisierung beim Drehratensensor
Für FC gilt:
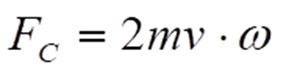
In MEMS-Sensoren wird FC nicht direkt gemessen. Es findet vielmehr eine kapazitive Messung der damit verbundenen Querauslenkung der Massen statt.
Beschleunigungssensoren
Die Messung einer Beschleunigung funktioniert heute bei fast allen diesbezüglichen Sensoren nach dem Trägheitsgesetz:
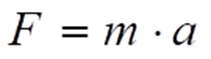
m wird hierzu als kleiner Massekörper realisiert, der an einer Federstruktur über das Sensorgehäuse am Messobjekt befestigt ist. Bei den meisten Sensorimplementierungen wird nun die bei Beschleunigung eintretende Auslenkung des Massekörpers gemessen, was z.B. kapazitiv geschehen kann. Eine alternative Bauart gehört zur Familie der piezoelektrischen Sensoren. Derartige Sensoren verwenden Quarze, die bei Druckausübung Ladungsträger freisetzen. In der Anwendung als Beschleunigungssensor kann ein solcher Quarz bereits für sich das Massenelement m darstellen. Drückt er bei Beschleunigung auf ein Teil des Sensorgehäuses, so wird der piezoelektrische Effekt initiiert. Je nach Messbereich werden aber auch separate Massen verbaut, die dann auf den Quarz drücken. Entscheidend für den Messeffekt ist die dabei wirkende Kraft selbst, es wird kein signifikanter Weg mehr zurückgelegt.
Inertiale Messeinheiten (IMU)
Es gibt eine steigende Zahl von Anwendungen, bei denen eine von äußeren Messeinrichtungen unabhängige Positionsbestimmung meist zum Zwecke der Navigation eingesetzt wird. Die hierzu verwendeten Sensorsysteme nennen sich inertiale Messeinheiten (engl. Inertial Measurement Unit, IMU). Die übergeordneten sog. inertialen Navigationssysteme werden mit INS (Inertial Navigation System) abgekürzt. Wichtige Anwendungen finden sich z.B. bei fahrerlosen Transportsystemen, Flugdrohnen und Gebäudenavigationssystemen (Indoor Positioning Systems, IPS).
Das Bild zeigt die grundlegende Idee. IMUs besitzen immer drei Beschleunigungssensoren für die drei Raumachsen sowie drei Drehratensensoren, welche die Drehraten um diese Raumachsen messen. Moderne Kompakt-IMUs sind relativ klein und benutzen in MEMS-Technologie gefertigte Sensoren. Die IMU ist über ihr Gehäuse fest mit dem Messobjekt, dessen Positionsänderung sie messen soll, verbunden. Die sechs Sensoren werden mit hoher Messrate kontinuierlich ausgelesen. Daraus lässt sich über einen entsprechenden Algorithmus die Position in Form dreier Koordinaten, die sich auf ein Referenzkoordinatensystem zu Beginn der Bewegung beziehen, laufend berechnen.
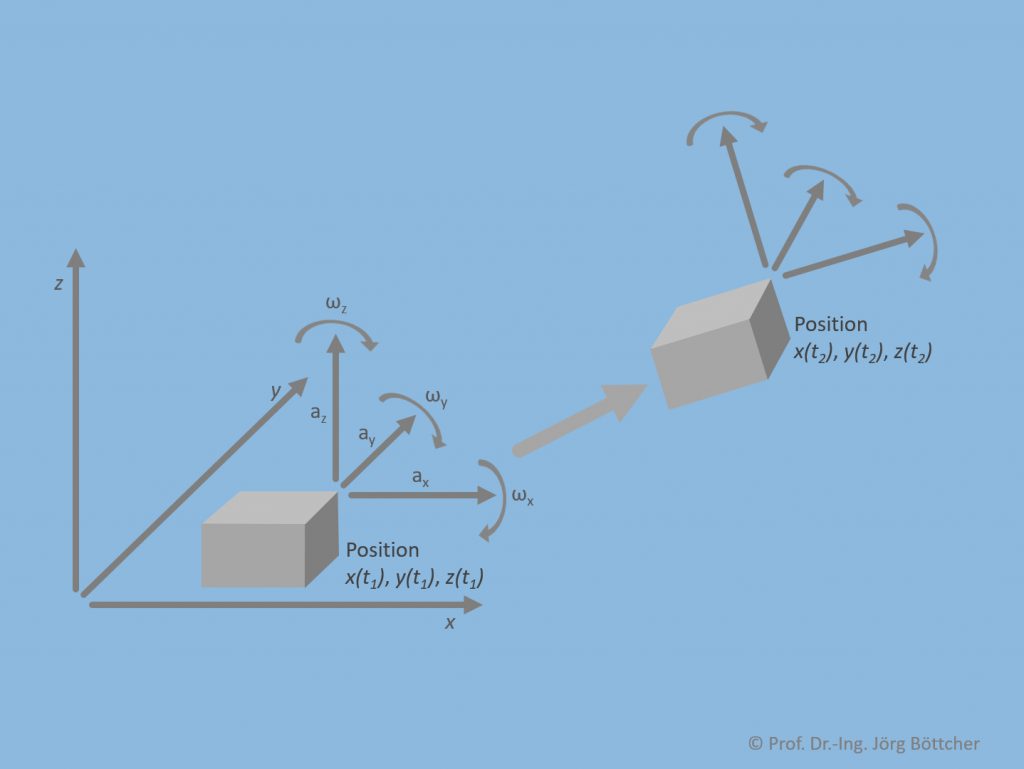
Grundprinzip einer IMU
Satellitennavigationssysteme
Zur Nutzung eines Satellitennavigationssystems werden entsprechende Chips bzw. darauf aufbauende Messmodule am Markt angeboten. Aktuell sind die Systeme
- NAVSTAR GPS (Navigational Satellite Timing and Ranging – Global Positioning System, meist kurz GPS genannt), USA
- GLONASS (Global Navigation Satellite System), Russland
- Galileo, Europa
- Beidou („Großer Bär“, abgekürzt auch BDS), China
im Einsatz (letztere beide noch nicht im Endausbau). Alle Systeme arbeiten nach demselben Messprinzip. In einem Orbit um die Erde verteilt befindet sich ein Verbund aus Satelliten, die in gewisser Taktung jeweils eine einheitliche Systemzeit, die aus Atomuhren an Bord gewonnen wird, und ihre jeweilige Position aussenden. Die Empfangselektronik am Boden muss nun die Signale von mindestens vier Satelliten für eine präzise Positionsbestimmung empfangen. Da sie eine eigene Zeitbasis besitzt, kann sie für das Datenpaket jedes Satelliten die entsprechende Sendezeit t1 bis t4 ermitteln und hierüber auf die dazu proportionalen Satellitenabstände schließen. Rein geometrisch betrachtet wären für eine Positionsbestimmung im Raum an sich nur drei Satelliten notwendig. Da die Zeitbasis des Empfängers aber deutlich ungenauer ist als die atomuhrbasierte an Bord der Satelliten, wird der vierte Satellit genutzt, um die Empfängerzeit immer wieder exakt auf die Systemzeit zu synchronisieren.
WENN SIE ES GENAUER WISSEN WOLLEN: