WENN SIE ES GENAUER WISSEN WOLLEN:

Im Folgenden geht es um zwei im Rahmen der Inbetriebnahme von Reglern relevante und miteinander zusammenhängende Aspekte. Der erste betrifft die Frage, welche Grenzbedingungen wir bei der Einstellung des Reglers beachten müssen, damit der Regelkreis stabil bleibt. Unter einem instabilen Regelkreis versteht man, dass dieser von innen heraus, fast schon wie ein elektrischer Oszillator, eine Schwingung mit größeren Amplituden über einen signifikanten Teil des Arbeitsbereichs generiert. Dies kann, muss aber nicht, durch eine spezifische äußere Anregung initiiert werden. Der zweite Aspekt ist die sinnvolle Wahl der am Regler einzustellenden Parameter, so dass der Regelkreis ein möglichst gutes Führungs- und Störverhalten zeigt. Für einen dieser Parameter, die Reglerverstärkung, gibt die zuvor durchgeführte Stabilitätsbetrachtung mitunter eine maximale Obergrenze vor, wie wir sehen werden. Die Ausführungen beziehen sich schwerpunktmäßig auf die Arbeit mit stetigen Reglern, i.d.R. also mit PID-Reglern.
Schwingbedingung
Instabile Schwingungen im Regelkreis beginnen immer mit einer „Urschwingung“, einer ersten mehr oder weniger sinusförmigen Schwingungsperiode an beliebiger Stelle im Kreis, die zufällig erzeugt wird. Diese kann z.B. ein Teil der ganz normalen Regelschwingung sein, wie sie im praktischen Regelungsbetrieb laufend an allen Signalstellen im Regelkreis zu beobachten ist. Oder sie kann von außen über eine Sollwert- oder eine Störgrößenänderung spontan eingebracht werden; insbesondere Sprünge enthalten (wenn man sie einer Spektralanalyse unterzieht) mehr oder weniger Elementarschwingungen über den kompletten Frequenzbereich.
Eine solche Schwingung baut sich auf, wenn die Urschwingung einer bestimmten Kreisfrequenz bei ihrem Umlauf einmal um den gesamten Regelkreis herum in gleicher Phasenlage wieder ankommt und dabei auch noch eine Verstärkung erfahren hat. In diesem Fall findet eine positive Interferenz statt. Mit jedem weiteren Umlauf verstärkt sich die Amplitude immer weiter bis zu einem durch die Arbeitsbereiche einzelner Regelkreiskomponenten begrenzten Maximum. Nur solche spontanen Schwingungen, für deren Kreisfrequenz diese zwei Teilbedingungen erfüllt sind, können als Urschwingung fungieren. Nur mit einer solchen Kreisfrequenz wird auch die endgültige große Schwingung schwingen.
Zu berücksichtigen ist dabei, dass die Bildung der Regeldifferenz stets eine Phasenverschiebung von (in Grad ausgedrückt) -180° produziert, also eine Phasenumkehr. Der Betrag des Signals wird hierbei nicht verändert, die Verstärkung an dieser Stelle ist also 1. Beides gilt für alle Frequenzen. Dies bedeutet, dass die Schwingbedingung für eine Frequenz dann erfüllt ist, wenn die vier verbleibenden Komponenten im Regelkreis zusammen ebenfalls eine Phasenverschiebung von -180° (bzw. auch -540°, -900°, -1.260° etc.) haben und deren Summenverstärkung größer als 1 ist.
Instabile Regelkreise
Unteres Bild zeigt das Simulationsergebnis einer mit einem reinen P-Regler geregelten PT1Tt-Strecke. Der Verstärkungsfaktor des Reglers sowie die Streckenparameter sind in der Bildunterschrift angegeben.
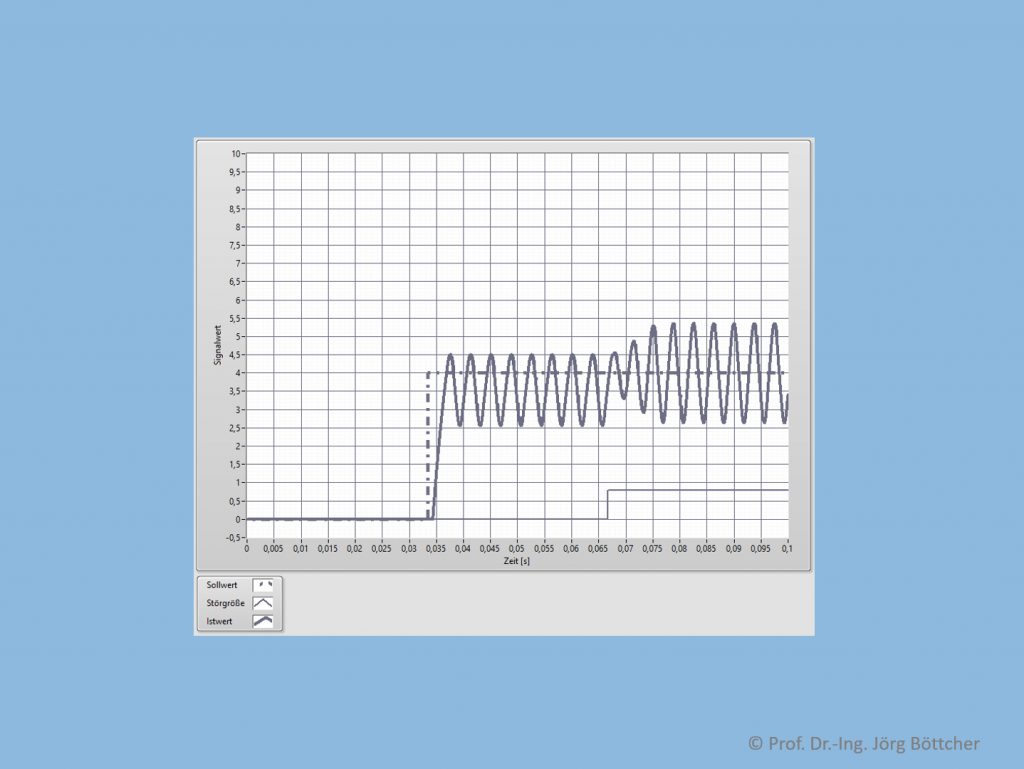
Regelkreis mit P-Regler (kR = 2) und PT1Tt-Strecke (kP = 5, T1 = 5 ms, T = 1 ms)
Nach dem simulativen Einschalten verhält sich der Regelkreis noch stabil und erzeugt einen Istwert, der dem gewünschten Sollwert von zunächst 0 entspricht. Sobald wir uns jedoch sprungförmig einen neuen Sollwert wünschen, bildet sich eine markante Sinusschwingung mit einer Amplitude, die das Maß üblicher Regelschwingungen deutlich übersteigt.
Würde man den Frequenzgang (ohne die Regeldifferenzbildung), beispielsweise als Nyquist-Diagramm, betrachten, so ließe sich dieses instabile Verhalten auch begründen: Bei grob etwa 250 Hz liegt die Phasenverschiebung bei -180°. Um diese Frequenz herum liegen aber die Verstärkungen über 1, was bedeutet, dass die Schwingbedingung hier erfüllt ist. Genau diese Frequenz sieht man auch in der Schwingung im Bild (wenn man z.B. 4 ms als Periodendauer abliest).
Stabilitätskennzahlen
Es empfiehlt sich, den Regelkreis so auszulegen, dass immer eine großzügige Reserve zur Stabilitätsgrenze hin besteht. Wie oben schon festgestellt, ist das Mittel der Wahl eine Begrenzung der Reglerverstärkung (insofern der Regelkreis überhaupt die Schwingbedingung erfüllen kann, was bei einfacheren Regelkreisen, die z.B. die geforderte Phasenverschiebung gar nicht erreichen, nicht der Fall ist).
Man hat hierzu zwei Stabilitätskennzahlen definiert: Die Amplitudenreserve ist der Kehrwert des Verstärkungswerts zu der Frequenz, bei der die Phasenverschiebung -180° beträgt. Eine Verstärkung von z.B. 0,6 entspräche einer Amplitudenreserve von knapp 1,7. In der Praxis fordert man gerne mindestens 2, was eine Verstärkung von 0,5 wäre.
Die Phasenreserve erhält man, wenn man zunächst die Phasenverschiebung sucht, bei der die Verstärkung 1 ist. Der Winkelabstand zu -180° ergibt dann die Phasenreserve. Die Praxisforderung lautet mindestens 30°.
Bei üblichen Frequenzgängen kann man durch eine Herabsetzung der Verstärkung des Reglers stets eine Verbesserung von Amplituden- und Phasenreserve herbeiführen bzw. instabile Regelkreise überhaupt erst stabil machen.
Praktische Einstellregeln
Für nicht zu kompliziertes Streckenverhalten haben etliche Autoren in der Vergangenheit Empfehlungen veröffentlicht, wie man optimale Reglerparameter für den PID-Regler (bzw. Untervarianten von ihm) ermittelt. Etliche sind sehr mathematisch und in der Praxis eher nicht gut verwendbar. In der Praxis haben sich insbesondere die in nachfolgendem Bild aufgeführten Verfahren sehr bewährt. Ausgangspunkt bildet eine theoretische oder experimentelle Untersuchung des Streckenverhaltens mit einer zumindest groben Abschätzung der signifikanten Streckenparameter, in diesem Zusammenhang auch als Ersatzparameter der Strecke bezeichnet.
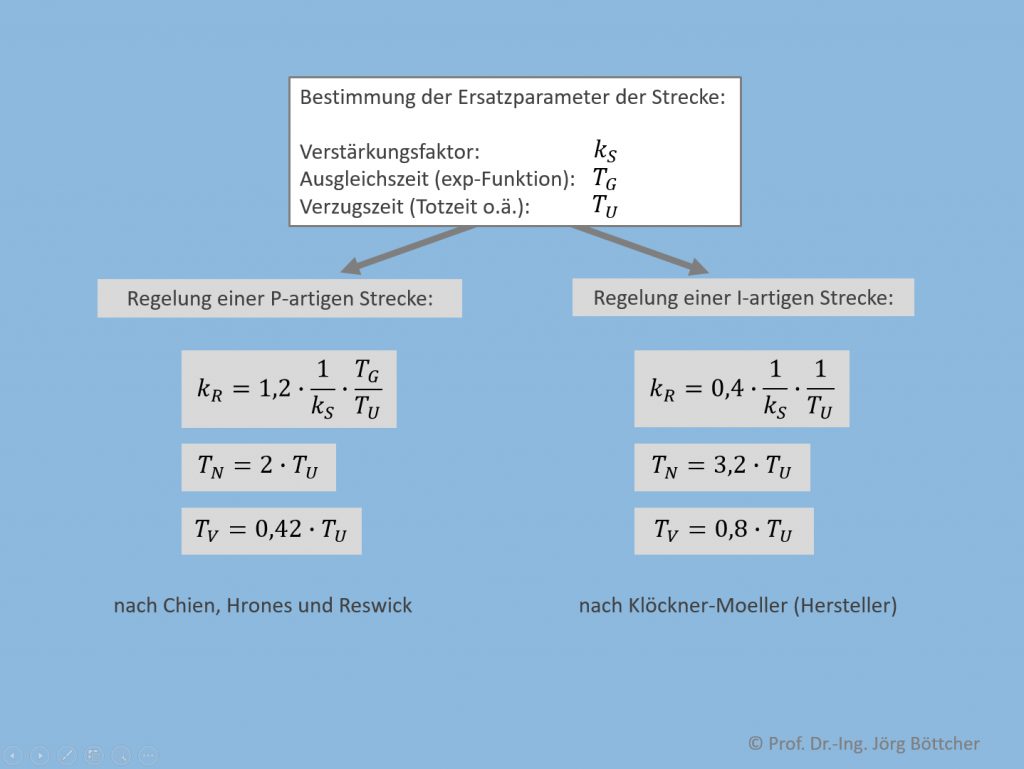
Praktische Einstellregeln über Ersatzparameter der Strecke
Die bekanntesten Einstellregeln, jedoch aus Sicht des Autors in der Praxis oftmals nicht so hilfreich wie die oben genannten, sind die von den Forschern J. G. Ziegler und N. B. Nichols bereits 1942 publizierten Einstellregeln, die ein konkretes Experiment am realen Regelkreis benötigen. Sie sind jedoch nur für proportionale („P-artige“) Strecken anwendbar. Nach diesen Vorgaben muss man die Strecke zunächst mit einem P-Regler mit kleinem Verstärkungsfaktor regeln und diesen so lange schrittweise erhöhen, bis der Regelkreis instabil wird, was sich in einer Dauerschwingung mit relativ großen Amplituden zeigt. In Abhängigkeit des dann erreichten Verstärkungsfaktors und der zu messenden Schwingperiode stellt man entsprechend eines Formelsatzes dann den PID-Regler selbst ein. Von der Einschränkung auf proportionale Strecken abgesehen, können diese Einstellregeln auch nur dann angewandt werden, wenn ein Regelkreis überhaupt instabil werden kann (und man dies in der Praxis auch ohne Gefahr durchführen darf).
In jedem Fall kann man sich heute durch moderne Tools, wie dem in diesem Kompendium benutzten LabVIEW, sehr viel trial-and-error-Aufwand sparen, wenn man einen Regelkreis vorab simuliert und dabei die Reglerparameter optimiert.
WENN SIE ES GENAUER WISSEN WOLLEN: