EIN
KOMPAKTER ÜBERBLICK
Thema dieses Überblicks ist der Zusammenhang zwischen Messgröße und Messwert in Form der sog. Kennlinie. Darauf basierend definiert der Messtechniker auch entsprechende Messabweichungen. Das Wissen darüber dient beispielsweise dazu, entsprechende Herstellerangaben korrekt zu interpretieren. Auch wird kurz darauf eingegangen, wie wir mit etwas Zusatzaufwand Messabweichungen durch Kalibrierung bzw. wiederholtes Messen verringern können.
Struktur eines Messsystems
Nachfolgendes Bild zeigt am Beispiel eines direkt den Messwert anzeigenden Temperaturmesssystems, wie ein solches strukturell typischerweise aufgebaut ist. Da es sich hier um eine nicht elektrische Messgröße handelt, wird zunächst ein Sensor benötigt, der ein mit der Messgröße xw korreliertes elektrisches Signal, z.B. eine elektrische Spannung, generiert. Dieses elektrische Primärsignal ist mitunter relativ klein und muss deshalb vielleicht noch verstärkt werden, bevor es einer Digitalisierung zugeführt wird. Die Digitalisierung wandelt das analog vorliegende elektrische Signal in ein korrespondierendes Digitalwort um, das durch Algorithmik digital weiterverarbeitet werden kann. Oftmals dient die digitale Signalverarbeitung einer Korrektur von auf der Analogseite befindlichen Unzulänglichkeiten, insbesondere von nichtidealen Kennlinien. Ausgegeben wird schließlich ein Messwert xa.
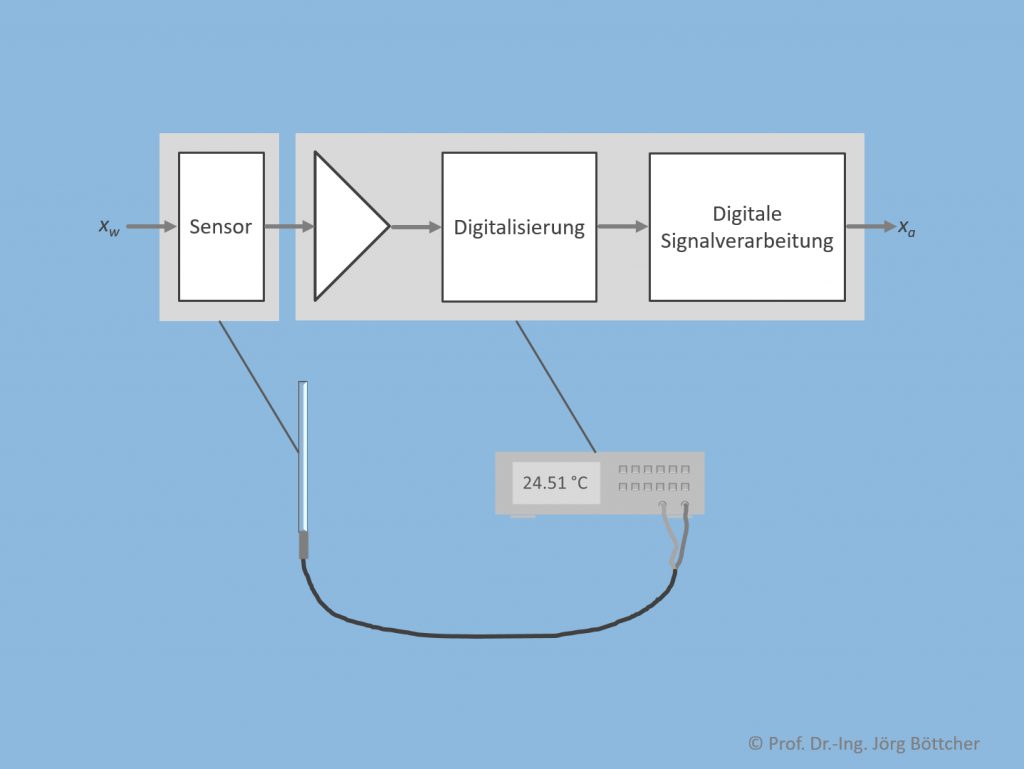
Struktur eines Messsystems
Kennlinien
Jede einzelne der Komponenten führt das jeweilige Eingangssignal in ein Ausgangssignal über, wobei der Zusammenhang durch eine Kennlinie angegeben werden kann. Für den Sensor ist eine solche Kennlinie in unterem Bild aufgeführt. Abgesehen von noch zu diskutierenden anderen Kennlinieneigenschaften ist es stets vorteilhaft, wenn die Kennlinie im gesamten Messbereich eine gewisse Steilheit besitzt. Anders ausgedrückt: Änderungen der Messgröße ϑw sollen auch zu einer deutlichen Änderung der Spannung U führen. Mathematisch ausgedrückt entspricht die Steilheit an einer bestimmten Stelle ϑw der Ableitung der Ausgangsgröße U(ϑw) nach ϑw gemäß
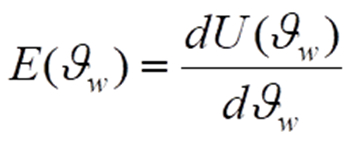
in der Messtechnik generell Empfindlichkeit E genannt. Grafisch kann man bekannterweise diese Ableitung auch als Steigung der Tangente an der jeweiligen Stelle ϑw begreifen, so wie dies im Bild dargestellt ist.
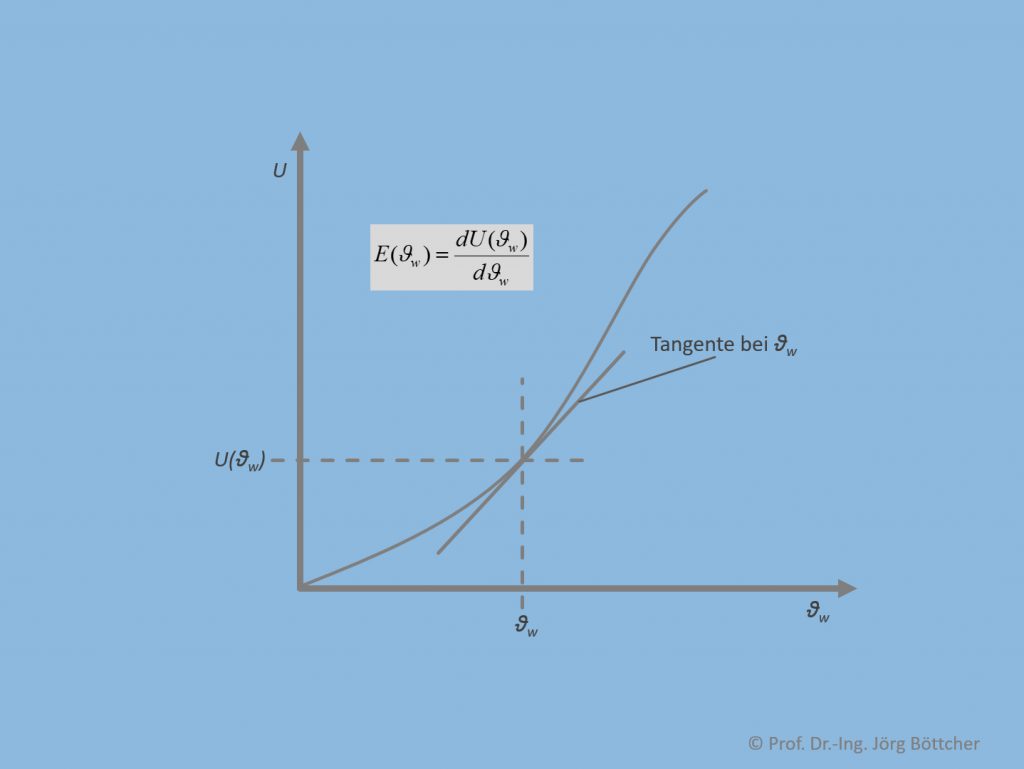
Kennlinie am Beispiel eines Temperatursensors
Im Messsystem werden nun sozusagen die Kennlinien jeder einzelnen Komponente hintereinander „geschaltet“, so dass eine das gesamte Messsystem beschreibende Kennlinie daraus resultiert.
Messabweichungen
Zu jeder Messgröße xw existiert eine Messabweichung
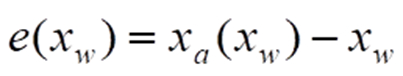
Die Abkürzung „e“ hat sich in vielen Publikationen hierfür fest eingeführt. Sie stammt vom englischen „error“ – auf Deutsch „Fehler“ – ab, dem im Angelsächsischen hierfür dominierenden Fachbegriff. Messabweichungen haben verschiedenste Ursachen: Zunächst hängen diese sehr stark vom Geschick und Aufwand ab, die der Hersteller bei Entwicklung und Fertigung investiert. Er kann jedoch nicht verhindern, dass anwendungsseitig sog. Störgrößen ebenfalls einen deutlichen Einfluss auf die konkrete Kennlinie ausüben. Die wichtigste Störgröße ist meist die Umgebungstemperatur. So zeigen die meisten in Sensoren angewandten physikalischen (bzw. chemischen) Prozesse eine mehr oder weniger ausgeprägte Abhängigkeit von ihr.
Die Angabe von Messabweichungen in der Praxis
Die Hersteller unterteilen mitunter die Spezifikation der messsystemseitig zu erwartenden worst case-Messabweichung in einzelne Effekte wie Nullpunktabweichung, Steigungsabweichung, Nichtlinearität und Hysterese. Messabweichungen findet man weiterhin häufig auch als Relativangabe in Prozent („±1,3 %“) bzw. Teilen davon (Promille „‰“ oder parts per million „ppm“). Relative Messabweichungen erel ergeben sich aus den entsprechenden Absolutabweichungen e gemäß
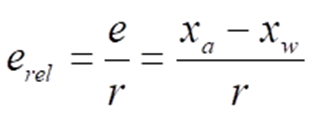
r ist hierbei ein Referenzwert, für den der Messwert selbst, die sog. Spanne oder der Messbereichswendwert üblich sind. Speziell bei Labormessgeräten (wie Multimetern) werden bei entsprechenden Angaben zu Messabweichungen bisweilen auch sog. Digits benutzt. Unter einem Digit ist die Wertigkeit der letzten numerischen Stelle des Anzeigewerts im Display zu verstehen. Bei einer Displayanzeige „12.702 V“ wäre ein Digit also 0,001 V (und nicht die an dieser Stelle angezeigten 0,002 V etwa).
Korrektur systematischer Messabweichungen
Der Anwender eines Messsystems kann bei Bedarf durch vorherige Kalibrierschritte die zu erwartenden Messabweichungen teilweise noch deutlich reduzieren. Voraussetzung ist, dass die zugrunde liegenden Einflusseffekte grundsätzlich reproduzierbar sind, also gewissen physikalischen Gesetzmäßigkeiten unterliegen, auch wenn diese dem Anwender nicht bekannt sein müssen. Wir sprechen von sog. systematischen Messabweichungen.
Nun jedoch zu den Korrekturverfahren für systematische Messabweichungen: Am häufigsten und auch am einfachsten durchführbar ist die sog. Nullpunktkorrektur (auch „Offsetkorrektur“ genannt). Für eine Nullpunktkorrektur muss zunächst einmalig z.B. bei der Erstinbetriebnahme an einem Kalibrierpunkt eine definierte Messgröße durch geeignete Maßnahmen erzeugt werden. Die so gewonnene Nullpunktabweichung muss bei allen nachfolgenden echten Messungen vorzeichenrichtig korrigiert werden. Sämtliche Änderungen in den Betriebsbedingungen gegenüber dem Kalibrierzeitpunkt wie auch z.B. Drifteffekte führen zu einer Verschlechterung dieser Korrekturmaßnahme, was Rekalibrierungen in angemessenen Zeitabständen sinnvoll machen kann.
Mehr Aufwand erfordert die kombinierte Nullpunkt- und Steigungskorrektur. Es sind zwei Kalibriermessungen erforderlich. Zusätzlich zur Messung am Nullpunkt ist noch ein zweiter Kalibrierpunkt zu wählen, meist wird hierfür der Messbereichsendwert gewählt. Ziel der Korrekturrechnung für den nachfolgenden echten Messbetrieb ist es, dass unter den Betriebsbedingungen zum Kalibrierzeitpunkt die reale Kennlinie so vertikal verschoben und um ihren Nullpunkt gedreht wird, dass für die beiden Kalibrierpunkte keine Messabweichungen mehr existieren.
Korrektur statistischer Messabweichungen
Wer den im Display eines Multimeters angezeigten Messwert einer beliebigen Gleichgröße (z.B. der konstanten Spannung einer Batterie) über einen gewissen Zeitraum beobachtet, wird feststellen, dass sich mitunter die letzten numerischen Stellen mehr oder weniger zufällig laufend verändern. Die Ursachen liegen hierbei typischerweise in elektronischen Rauschvorgängen des analogen Schaltungsteils des Multimeters sowie in elektromagnetischen Einstreuungen der wie eine Antenne wirkenden Anschlussleitungen. Gleiches gilt generell für die meisten Messprozesse, insofern analoge elektrische Signale zu verarbeiten sind, also auch für sämtliche Systemlösungen mit z.B. PC-Messkarten bzw. -modulen.
Die überwiegende Mehrzahl der diesbezüglichen Wahrscheinlichkeitsverteilungen in der Messtechnik nähert sich für einen größere Anzahl N an Messungen zumindest grob der bekannten Normalverteilung (auch Gaußverteilung genannt) mit ihrer charakteristischen Glockenform an. Eine Verteilung hat einen Mittelwert und eine sog. Standardabweichung s. Bei einer echten Normalverteilung liegen ca. 99,7 % aller Messwerte in einem Bereich von ±3s, weshalb der Messtechniker dies auch als statistische worst case-Messabweichung definiert.
Wir können nun auch statistische Messabweichung zumindest um einen substanziellen Anteil minimieren. Immer dann, wenn im normalen Messbetrieb eine Messung zeitlich ansteht, führen wir hierzu eine Sequenz von N Einzelmessungen durch und berechnen uns aus den zugehörigen N Messwerten den Mittelwert. Man kann zeigen, dass die so gewonnenen Mittelwerte ihrerseits auch einer Normalverteilung unterliegen. Die zugehörige Standardabweichung ist jedoch deutlich kleiner als die Standardabweichung s der Einzelmessungen. Es gilt:
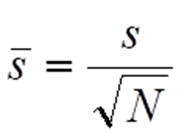
Für N = 10 ergibt sich beispielsweise bereits eine Reduktion der Standardabweichung und damit auch der statistischen Messabweichung auf etwa 31,6 %, also grob um den Faktor 3.
Fortpflanzung von Messabweichungen
Bei vielen messtechnischen Aufgabenstellungen – beispielhaft seien rechnergesteuerte Prüfstände genannt – werden die zugehörigen Messwerte mit Hilfe mathematischer Zusammenhänge miteinander verrechnet, um auf das eigentlich interessierende sog. Messergebnis zu kommen (siehe Bild). Dieses ist in Abhängigkeit der Messabweichungen der einzelnen Messwerte sowie der Berechnungsvorschrift ebenfalls mit einer Messabweichung behaftet.
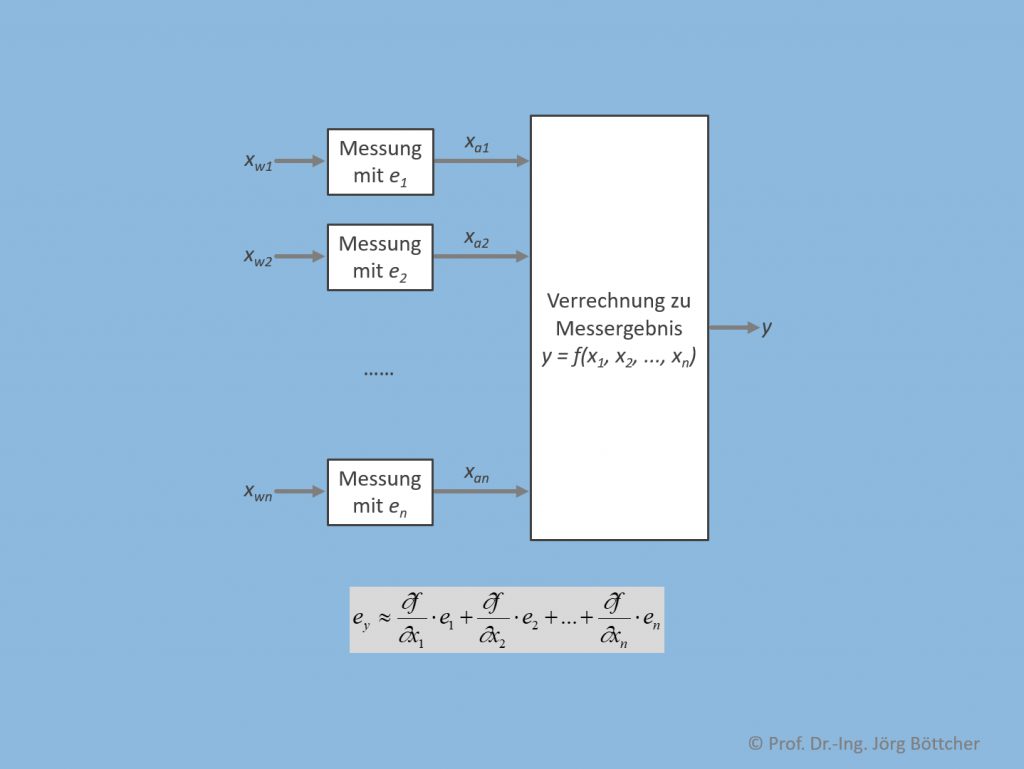
Verrechnung mehrerer Messungen zu einem Messergebnis
Bei sehr einfachen funktionalen Zusammenhängen mit nur wenigen zu verrechnenden Messwerten kann man den worst case der Messabweichung für das Messergebnis rein durch „Hinschauen“ ermitteln. Wird z.B. eine elektrische Leistung durch separate Messung von Spannung und Strom ermittelt, wobei wir als Messwerte 10 V bzw. 1 A annehmen, ergibt dies eine Leistung von 10 W. Unterstellen wir maximale Messabweichungen von im Betrag 0,05 V (entspricht 0,5 % Relativabweichung, bezogen auf den Messwert) bzw. 0,02 A (entspricht 2 % Relativabweichung, bezogen auf den Messwert), so können die zugehörigen Messwerte in den Intervallen [9,95 V … 10,05 V] bzw. [0,98 A … 1,02 A] liegen. Nach Multiplikation ergibt sich somit ein mögliches Intervall [9,751 W … 10,251 W] für die Leistung, was einer Messabweichung im worst case von etwa 0,25 W entspricht bzw. relativ 2,5 %. In diesem speziellen Fall einer Multiplikation als Berechnungsvorschrift addieren sich die relativen Messabweichungen.
Für kompliziertere Zusammenhänge mit mehreren Messgrößen lassen sich worst case-Kombinationen nicht mehr so einfach erkennen. Hier geht man auf eine mathematische Berechnung unter Verwendung der Einzelempfindlichkeiten der Berechnungsfunktion bezogen auf die jeweilige Messgröße über.
WENN SIE ES GENAUER WISSEN WOLLEN: