WENN SIE ES GENAUER WISSEN WOLLEN:

Verknüpft man physikalische Elementarprozesse der Art, wie wir sie im letzten Kapitel angesprochen haben, zu Gesamtsystemen mit einer Eingangs- und einer Ausgangsgröße, so erhält man ein sog. lineares System. Wir wollen dies nachfolgend anhand eines sehr einfachen mechanischen Systems demonstrieren. Im Buch selbst wird dies ausführlicher und vor allem auch mit weiteren Beispielen u.a. aus dem Bereich elektrischer bzw. hydraulischer Systeme behandelt. Wie wir sehen werden, münden diese Betrachtungen immer in eine sog. lineare Differentialgleichung n-ter Ordnung. Um vorschnellen Befürchtungen entgegen zu treten: Wir werden nicht in die Mathematik des Lösens derartiger Gebilde einsteigen. Vielmehr benutzen wir diese als Ausgangspunkt für Simulationen, wie wir sie in späteren Kapiteln dieses Kompendiums behandeln. Das Aufstellen der Differentialgleichungen selbst benötigt nicht mehr als die vier Grundrechenarten und einfaches Basiswissen zum Ableiten bzw. Integrieren.
Beispiel: Mechanisches Dämpfer-Masse-System
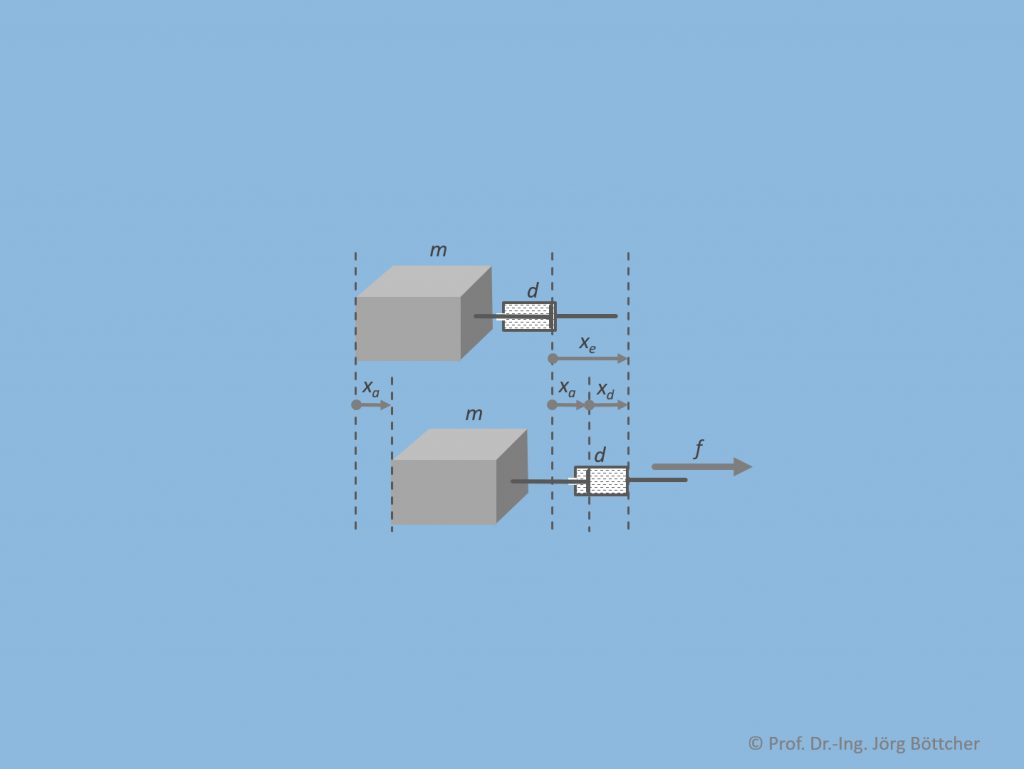
Betrachten wir das System im Bild. Eine Masse m werde über einen Dämpfer mit dem Dämpfungsbeiwert d in einer Dimension beschleunigt. Eingangsgröße sei die Positionsänderung xe, welche durch eine Krafteinwirkung f – welche im Ergebnis jedoch nicht weiter interessieren soll – bewirkt wird. Ausgangsgröße sei die dabei beobachtete Positionsänderung xa der Masse selbst.
Dämpfer-Masse-System
Hierzu lassen sich zwei Elementgleichungen und eine Maschengleichung aufstellen (siehe letztes Kapitel):
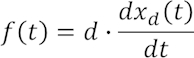
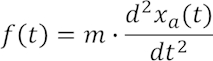
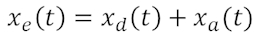
Die insgesamt aufgezwungene Positionsänderung xe teilt sich also auf in ein Aufziehen des Dämpfers xd sowie eine Positionsänderung der trägen Masse xa. xa ist im Bild zweifach, einmal an der Masse selbst, weiterhin am gegenüberliegenden Ende der starren Befestigung zum Dämpfer hin, eingezeichnet, so dass die Verknüpfung der drei Positionsänderungen im Sinne einer Masche besser zu erkennen ist.
Diese Formeln ineinander eingesetzt, ergeben schließlich:
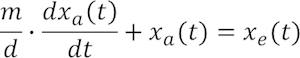
Der Quotient aus m (Einheit kg) und d (Einheit N/(ms-1)) als erster Parameter auf der linken Seite ist eine Zeitkonstante, deren Bedeutung wir in Folgekapiteln noch kennenlernen werden.
Systemdifferentialgleichung
Verknüpfen wir physikalische Teilprozesse, so wie wir das in obigen vier Beispielen gemacht haben, ausschließlich mit den mathematischen Operationen Addition bzw. Subtraktion, Multiplikation bzw. Division mit einer Konstanten, Differenzieren sowie Integrieren, so erhalten wir stets ein sog. lineares System.
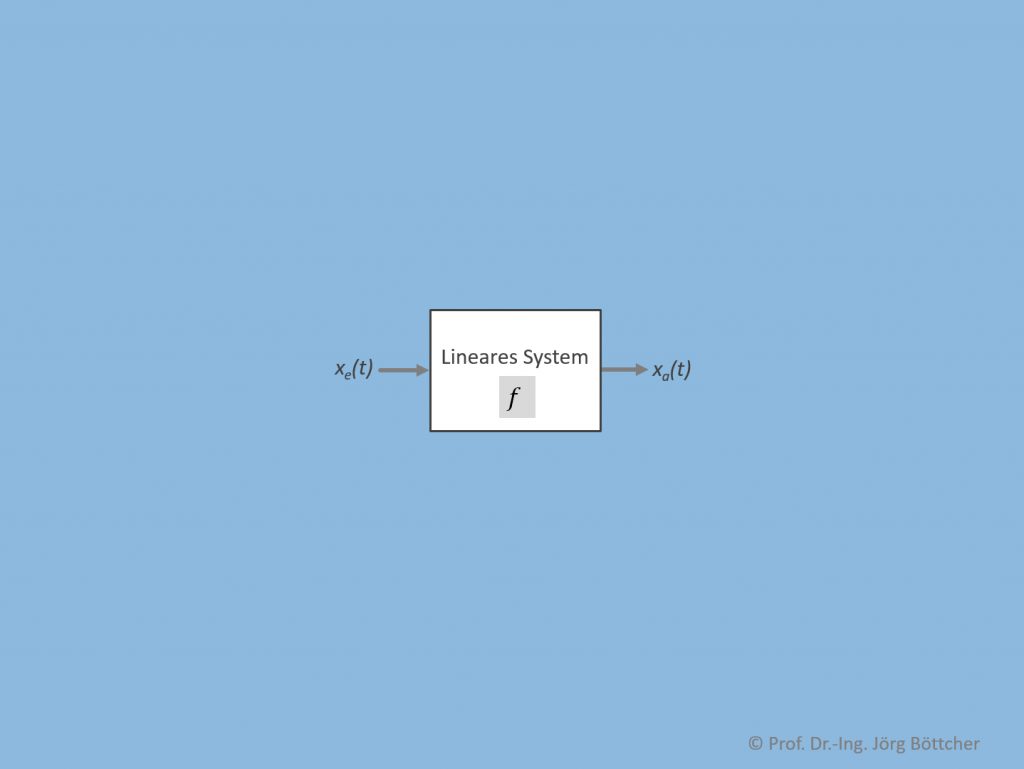
Lineares System
Es lässt sich bzgl. einer jeweils betrachteten Eingangs- und Ausgangsgröße xe(t) bzw. xa(t) mittels einer linearen Differentialgleichung beschreiben:
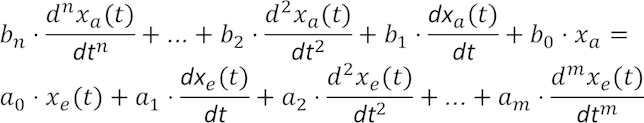
Lineare Systeme erfüllen das sog. Superpositionsprinzip
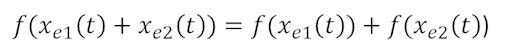
sowie das sog. Verstärkungsprinzip
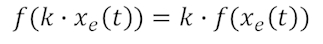
Ersteres bedeutet, dass man die Systemantwort auf ein zusammengesetztes Eingangssignal auch als Summe der Systemantworten zu jedem Teileingangssignal darstellen kann. Letzteres sagt aus, dass die Systemantwort eines mit einem Faktor multiplizierten („verstärkten“) Eingangssignals der Systemantwort des unverstärkten Eingangssignals entspricht, wenn man diese erst im Nachgang verstärkt. Diese beiden Voraussetzungen erfüllen selbstverständlich auch die zugrunde gelegten oben genannten mathematischen Operationen.
Linearisierung nichtlinearer Operationen
Bildet man technische Prozesse durch Simulationen nach, wie wir das in nachfolgenden Kapiteln tun werden, dann kann man dort selbstverständlich auch alle nichtlinearen Operationen in das Simulationsmodell aufnehmen. Möchte man dagegen eine dem realen Systemverhalten zumindest angenäherte mathematische Beschreibung erzielen, so ist dies bei Vorhandensein nichtlinearer Operationen sehr schnell äußerst aufwendig bzw. überhaupt nicht mehr geschlossen darstellbar. Insofern ist man in letzterem Fall bestrebt, das an sich nichtlineare Systemverhalten durch ein angenähertes lineares Verhalten zu beschreiben. Dazu werden sämtliche nichtlinearen Basisoperationen innerhalb des nachzubildenden Gesamtsystems durch Linearisierungen ersetzt.
WENN SIE ES GENAUER WISSEN WOLLEN: