WENN SIE ES GENAUER WISSEN WOLLEN:

Betrachtet man lineare bzw. linearisierte Modelle technischer Prozesse, so ist mitunter neben dem reinen Zeitverhalten das sog. Frequenzverhalten von Interesse. Während man unter ersterem versteht, welches Ausgangssignal das System bei Anlegen bestimmter Eingangssignale produziert, basiert letzteres auf der Annahme eines Sinussignals am Eingang. Das Sinussignal läuft durch das System hindurch und wird dabei bzgl. seiner Amplitude inkl. ggf. physikalischen Einheit verändert, was wir unten durch den hier verallgemeinert zu verstehenden Begriff „Verstärkung“ beschreiben. Weiterhin wird es beim Durchlauf durch reale Systeme stets verzögert, wie sprechen von einer Phasenverschiebung. Kennzeichnend für lineare Systeme ist, dass ein Sinussignal am Eingang eben auch am Ausgang zu einem Sinussignal gleicher Frequenz führt, also nicht zu einem periodischen Signal anderer Kurvenform oder gar einem nicht mehr periodischen Signal. Wir wollen nachfolgend im kurzen Überblick zeigen, wie wir im Rahmen der Systemsimulation mit LabVIEW das Frequenzverhalten einfach ermitteln können, sowie auf die mathematische Berechnung ausgehend von der Übertragungsfunktion der Laplace-Transformation eingehen.
Bode-Diagramm
Das Auftragen von Verstärkung und Phasenverschiebung über der Frequenz in zwei separaten Diagrammen nennt man „Bode-Diagramm“, benannt nach dem 1905 geborenen amerikanischen Elektrotechnik-Ingenieur und Forscher Hendrik Wade Bode. Zur Demonstration haben wir das aus dem letzten Kapitel bereits bekannte RC-Glied mit der Zeitkonstanten RC = 2 ms in LabVIEW, wie dort beschrieben, linearisiert und über die Funktionen „Bode Magnitude“ und „Bode Phase“ ausgewertet. Die Anzeigen der beiden zugehörigen Signalverlaufsgraphen zeigt nachfolgendes Bild. Die Diagramme nennen sich auch „Amplitudengang“ (obwohl nicht die Amplitude des Ausgangssignals als solche, sondern die Verstärkung aufgetragen wird) bzw. „Phasengang“, beide zusammen bilden den bereits angesprochenen, kompletten „Frequenzgang“ (oder eben das „Bode-Diagramm“).
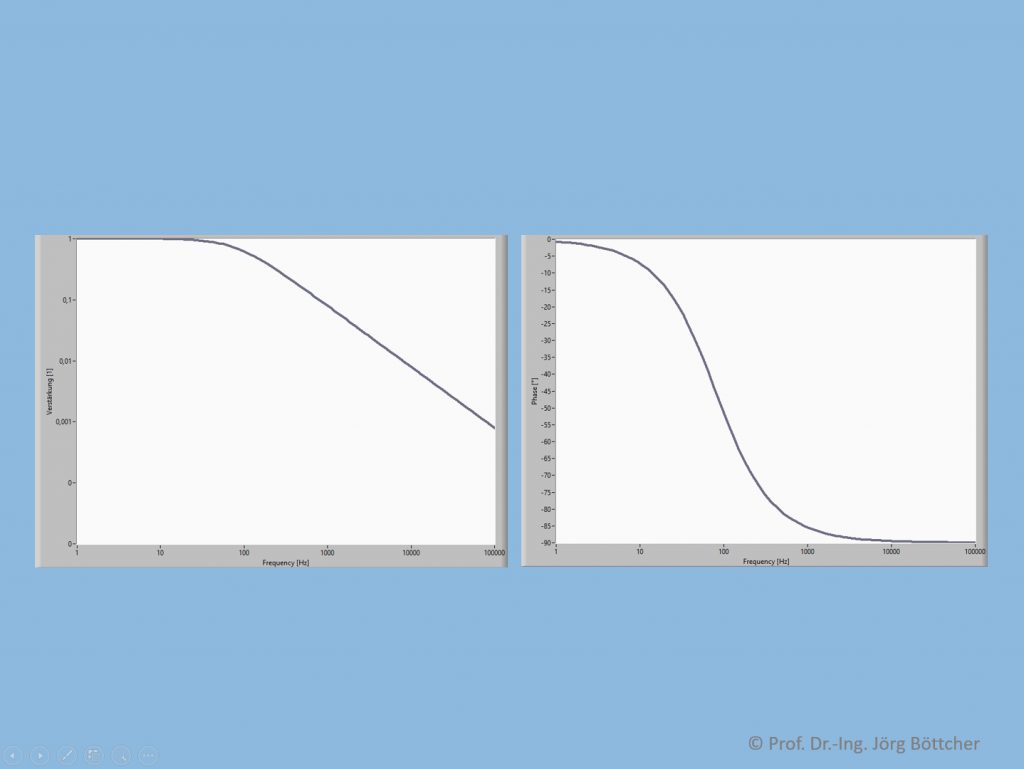
Amplitudengang und Phasengang zum RC-Glied mit RC = 2 ms
Elektrotechnisch vorgebildete Leser/-innen werden dieses Frequenzverhalten eines RC-Glieds gut nachvollziehen können. Bei sehr kleinen Frequenzen kann sich die Kapazität C „mühelos“ auf den jeweiligen Momentanwert des Eingangssinussignals aufladen. Die an ihr abfallende Ausgangsspannung ist bzgl. Amplitude und Phasenlage praktisch identisch mit dem Eingangssignal. Mit steigender Frequenz gelingt dies immer schlechter. Die Amplitude des Ausgangssignals und damit die Verstärkung nehmen ab, es kommt zu einem zunehmenden „Nachhinken“ der Ausgangsspannung, also einer Phasenverschiebung. Bei sehr hohen Frequenzen schließlich wirkt die Kapazität wie ein Kurzschluss, die Ausgangsspannung geht gegen 0. Sie verliert jedoch nicht ihren kapazitiven Effekt an sich, der sich in einer asymptotisch gegen -90 ° gehenden Phasenverschiebung äußert.
Nyquist-Diagramm
Nach dem 1889 in Schweden geborenen und später in die USA ausgewanderten Elektrotechnik-Ingenieur ist eine alternative Darstellung des Frequenzgangs benannt, welche Amplitudengang und Phasenverschiebung in einem gemeinsamen Diagramm vereint. Unteres Bild zeigt die über die entsprechende LabVIEW-Funktion erzeugte Darstellung, welche sich im deutschen Sprachgebrauch auch „Ortskurve“ nennt. Die drei gestrichelten Linien inkl. der drei Beschriftungen innerhalb der Diagrammfläche wurden manuell eingeführt.
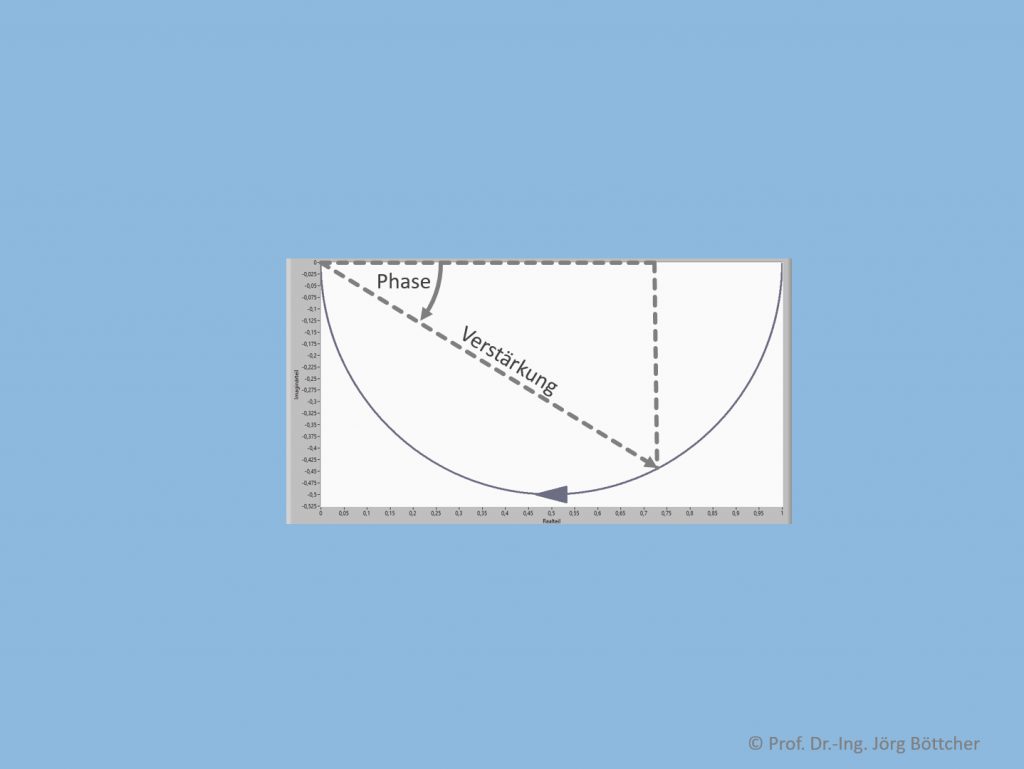
Nyquist-Diagramm (Ortskurve) zum RC-Glied mit RC = 2 ms
Rechnerische Herleitung am Beispiel RC-Glied
Am Beispiel des RC-Glieds des letzten Kapitels wollen wir betrachten, wie man den Frequenzgang auch mathematisch herleiten kann. Ausgangspunkt ist die Laplacesche Systemübertragungsfunktion, die wir z.B. aus der Differentialgleichung des Systems gewinnen können:
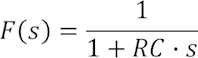
Die sog. komplexe Frequenzgangfunktion ergibt sich, in dem wir bei der komplexen Frequenz s den Realteil zu 0 setzen und nur noch den Imaginärteil schreiben:
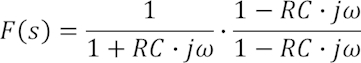
Um auf die für die weitere Rechnung benötigten Real- bzw. Imaginärteile von F(s) zu kommen, haben wir in dieser Formel gleich um den konjugiert komplexen Nenner erweitert. Daraus ergibt sich:
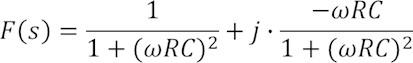
Der erste Summand stellt den Realteil dar, der zweite nach dem j den Imaginärteil. Der Amplitudengang ist nun der aus Real- und Imaginärteil zu berechnende Betrag:
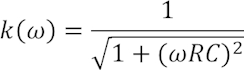
Der Phasengang entspricht dem Winkel (sog. Argument) zwischen Real- und Imaginärteil:
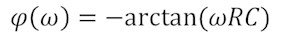
WENN SIE ES GENAUER WISSEN WOLLEN: