WENN SIE ES GENAUER WISSEN WOLLEN:

Einige elementare Übertragungsfunktionalitäten kommen in technischen Prozesse immer wieder vor, sei es in Form von Teilprozessen oder mitunter auch den Gesamtprozess charakterisierend. Wir wollen die wichtigsten derartigen, allesamt auch linearen Basisübertragungsglieder nachfolgend aufführen. In der ausführlichen Darstellung im Buch ist hierbei jedes Übertragungsglied detailliert und in gleicher Struktur beschrieben: Einer Darstellung des funktionalen Zusammenhangs zwischen Eingangs- und Ausgangssignal i.d.R. in Form einer linearen Differentialgleichung folgt deren Äquivalent im Spektralbereich, die auf der Laplace-Transformation basierende Systemübertragungsfunktion. Weiterhin wird die Systemantwort auf das typische Testsignal im Zeitbereich, die Sprungfunktion, analysiert und abschließend das Frequenzverhalten. Online ist nachfolgend nur das PT1-Glied leicht ausführlicher dargestellt, die anderen Glieder werden nur kurz aufgezählt.
Typ P
„P“ steht hierbei für proportionales Verhalten und kennzeichnet ein Übertragungsglied, welches das Eingangssignal mit einem festen, „eingebauten“ Faktor multipliziert:
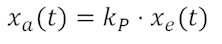
Man spricht auch vom „Verstärkungsfaktor“ kP des Übertragungsglieds. Dieser kann unabhängig von diesem Sprachgebrauch vom Betrag her jedoch auch kleiner als 1 sein, ein positives oder negatives Vorzeichen besitzen und über eine physikalische Einheit verfügen, die für die Umskalierung der Einheit der Eingangsgröße auf jene der Ausgangsgröße sorgt.
Typ PT1
Im Gegensatz zum eher nicht so oft in Reinform auftretenden Typ P handelt es sich hierbei um das wohl häufigste Basisübertragungsglied. Es zeichnet sich mathematisch dadurch aus, dass in der Zeitbereichsgleichung, die nun auch erstmals eine echte Differentialgleichung darstellt, eine Zeitkonstante T1 auftritt:
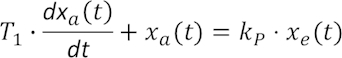
Die zugehörige Spektralgleichung lautet:
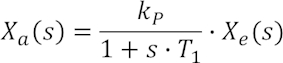
Das in früheren Kapiteln bereits häufiger angesprochene RC-Glied ist ein typisches Beispiel für PT1-Verhalten, insofern man die Summenspannung über beide Elemente als Eingangssignal und die Spannung an der Kapazität als Ausgangssignal verwendet. Ein Vergleich obiger beider Formeln mit den damals hergeleiteten zeigt, dass kP dabei den Wert von 1 aufweist, während T1 = RC ist.
Die Sprungantwort auf einen Eingangssprung auf xe,0 lautet:
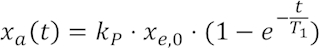
Speziell für xe,0 = 1, kP = 2 und T1 = 1 ms simuliert, ist dies ein Verlauf gemäß nachfolgendem Bild. Wir haben hier bewusst auf die Verwendung physikalischer Einheiten verzichtet. Charakteristisch für den hier vorhandenen exponentiellen Verlauf ist, dass nach Ablauf der Zeitkonstanten T1 ca. 63 % des Endwerts erreicht werden. Nach zwei/drei/fünf Zeitkonstanten sind es ca. 86/95/99 %.
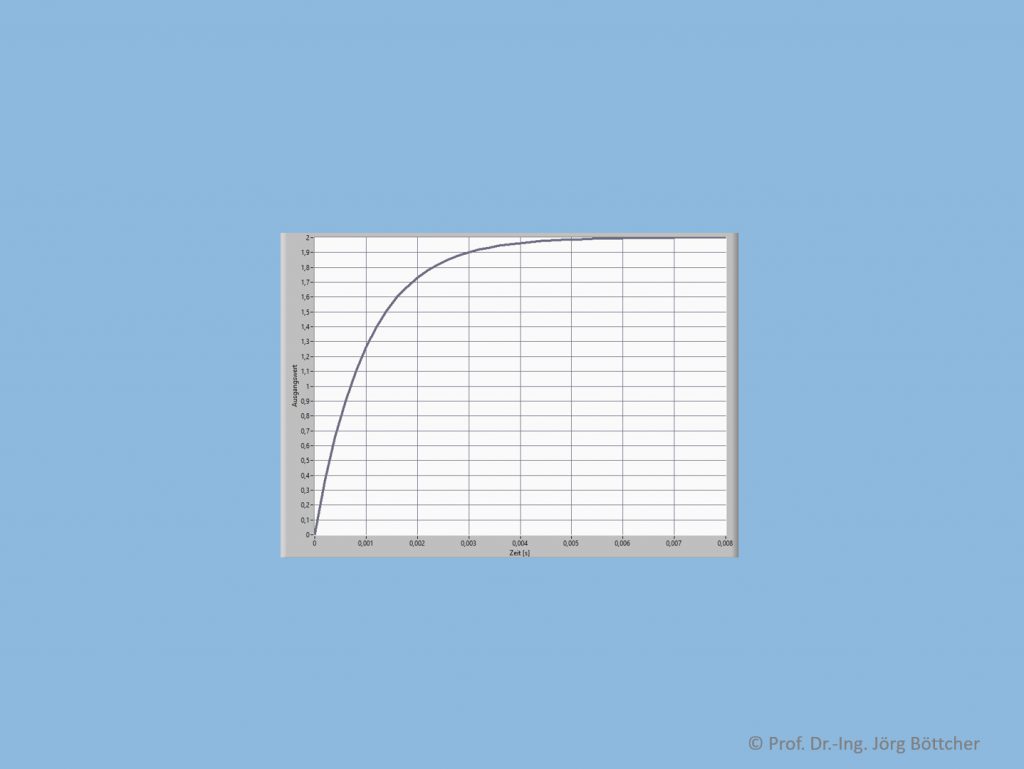
Sprungantwort eines PT1-Systems mit xe,0 = 1, kP = 2 und T1 = 1 ms
Im letzten Kapitel wurde das Frequenzverhalten für das RC-Glied hergeleitet. Im allgemeinen Fall eines PT1-Glieds mit einem Verstärkungsfaktor kP lautet es:
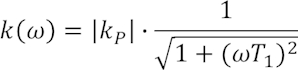
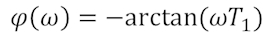
Markant ist dabei die Kreisfrequenz 1/T1, bei welcher die Verstärkung um einen Faktor einbricht, der dem Kehrwert der Wurzel aus 2 entspricht, und die Phasenverschiebung (in Grad ausgedrückt) -45° beträgt.
Typ PT2
Ein sehr interessantes Verhalten zeigen sog. PT2-Systeme, bei denen zusätzlich zur Zeitkonstanten des PT1-Systems noch eine zweite hinzugenommen wird, was sich in der Differentialgleichung durch eine zweite Ableitung äußert. Wir wollen die Differentialgleichung nicht mit den Zeitkonstanten selbst schreiben, sondern direkt in der üblicherweise verwendeten Darstellung mit Parametern, die wir in der Sprungantwort bzw. dem Frequenzgang besser erkennen:
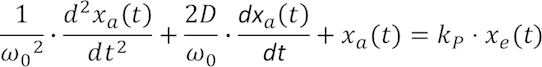
ω0 nennt sich „Kreisfrequenz der ungedämpften Schwingung“, D ist die sog. „Dämpfung“ (auch „Dämpfungsgrad“). kP bleibt die eingebaute Verstärkung, wie wir sie bereits von den beiden ersten Übertragungsgliedern kennen.
Typ D
Eher etwas seltener bei einem Basisübertragungsglied anzutreffen ist ein differenzierendes Verhalten. In idealer mathematischer Formulierung wäre dies
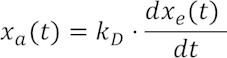
was physikalisch nicht zu realisieren ist. Ein Sprung im Eingangssignal würde hier zu einem unendlich hohen, unendlich kurzen Impuls führen. In der Praxis wird man differenzierendes Verhalten nur in Kombination mit einer Zeitkonstanten T1 antreffen.
Typ I
Im Gegensatz zu Basisübertragungsgliedern mit D-Verhalten sind solche mit integrierendem Verhalten, daher der Name „Typ I“, häufiger anzutreffen. Sie folgen, geschrieben in der Standardform einer linearen Differentialgleichung, der Formel
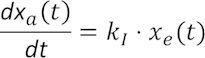
was nach Auflösung nach xa(t) die mit dem Faktor kI gewichtete Integration des Eingangssignals ergibt.
Totzeitglied
Dieses sehr einfach verständliche Übertragungsverhalten besteht aus einer reinen Verzögerung eines Signals um eine konstante Zeit, der sog. Totzeit T:
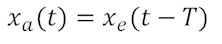
Häufige Kombinationen von Basisübertragungsgliedern
Zwei sehr oft vorkommende Serienanordnungen von Basisübertragungsgliedern wollen wir ganz kurz separat aufführen, obwohl sich deren Verhalten natürlich aus den beiden Einzelgliedern einfach ableiten lässt. Beide Kombinationen haben aufgrund ihrer Verbreitung eine eigene Typbezeichnung.
Ein PT1Tt-System besteht aus hintereinander angeordneten PT1-Glied und Totzeitglied. Die Reihenfolge ist egal. Beim zweiten wichtigen Kombinationstyp, dem IT1-System, werden ein I-Glied und ein PT1-Glied in Serie angeordnet (auch hier in beliebiger Reihenfolge).
WENN SIE ES GENAUER WISSEN WOLLEN: