WENN SIE ES GENAUER WISSEN WOLLEN:

Nachfolgend wird auf die mathematische Beschreibung wichtiger physikalischer Elementarprozesse exemplarisch und auszugsweise aus dem Bereich mechanisch-translatorischer Systeme eingegangen. Im Fachbuch selbst werden auch elektrische, mechanisch-rotatorische, hydraulische, pneumatische und thermische Elementarprozesse behandelt. Auch wenn die real vorhandenen Prozesse mitunter nicht exakt diesen idealen Ansätzen folgen, so kann man sie doch oftmals recht gut näherungsweise damit modellieren. In nachfolgenden Kapiteln werden wir dann auf die Verknüpfung dieser Elementarprozesse eingehen, um hierüber einen Gesamtprozess zu modellieren sowie sein Verhalten zu simulieren.
Mechanisch-translatorische Systeme
Bei mechanischen Systemen interessiert uns im Sinne der Simulation bzw. Regelung meist, wie sich Strecken – ob Wegstrecken oder Abstände – sowie Kräfte in ihrem zeitlichen Verlauf ändern. Zwischen der Kraft f(t) in der Einheit Newton (N) und der Strecke x(t) in der Einheit Meter (m) lassen sich für die drei wichtigsten Elementtypen mathematische Zusammenhänge formulieren, die denen ihrer elektrischen Pendants sehr ähneln. Wir wollen uns hierbei zunächst auf lineare Bewegungen (Translationen) in einer Dimension beschränken; mehrdimensionale Bewegungen lassen sich als Überlagerung dieser beschreiben.
Grundsätzlich lassen wir uns dabei von der Vorstellung leiten, dass Kräfte ähnlich dem elektrischen Strom quasi durch die Elemente hindurchfließen und sich an entsprechenden Knoten beispielsweise auch aufteilen können. Weiterhin sind Strecken immer zwischen zwei Punkten definiert, also gewissermaßen quer zu den Elementen, so wie wir das auch von elektrischen Spannungen her kennen. Die drei Elemente sind im Bild dargestellt.
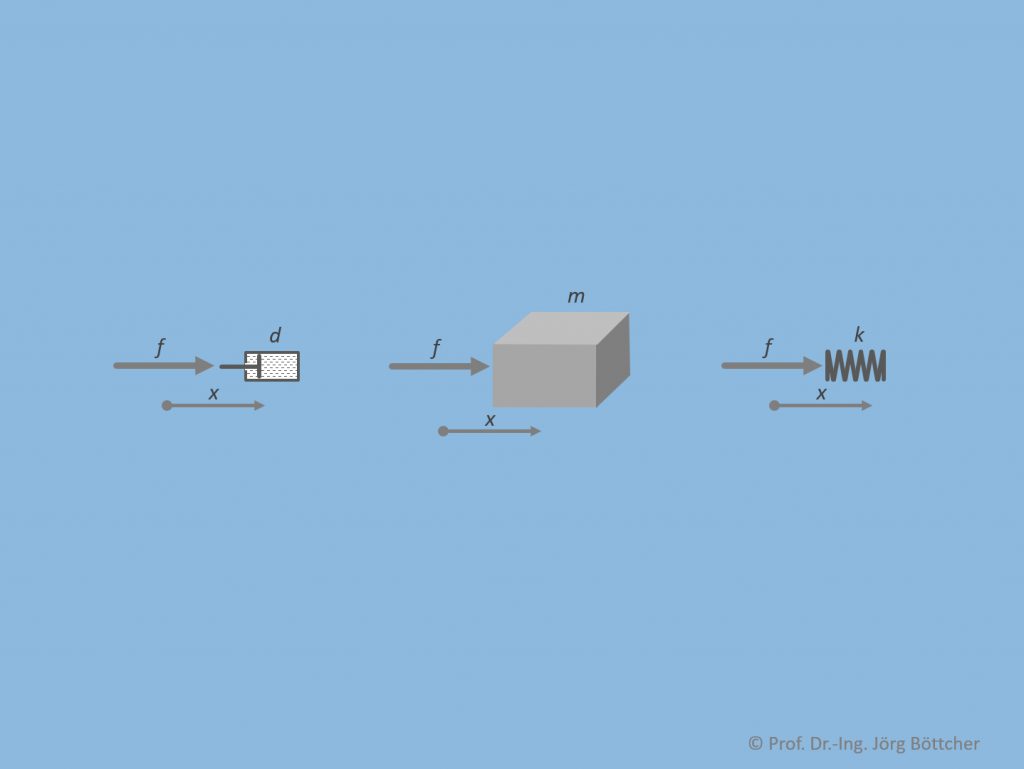
Dämpfer, Masse und Feder
Die mathematische Beschreibung der drei Elemente
Für einen Dämpfer mit dem sog. Dämpfungsbeiwert d gilt:
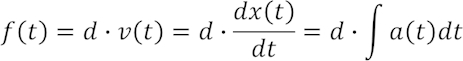
Für bewegte Massen m gilt das Newtonsche Trägheitsgesetz:
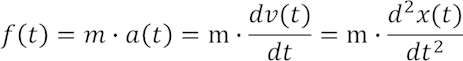
Für Federn ist das Hookesche Federgesetz mit k als Federkonstanten definiert:
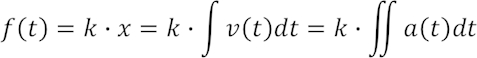
Obige drei Elemente können explizit so als Komponenten verbaut werden, wie dies beispielsweise bei der Radaufhängung eines Fahrzeuges über Feder und Dämpfer der Fall ist. Mitunter zeigen vorhandene konstruktive Teillösungen, die an sich anderen Zwecken dienen, jedoch auch ein dazu vergleichbares Verhalten. Als Beispiel hierfür sei – um beim Fahrzeug zu bleiben – das Fahrzeugchassis genannt, das an sich als Träger solcher Komponenten wie Motorblock und Fahrgastzelle dient, jedoch stets auch eine gewisse federnde Eigenschaft hat, welche entsprechend durch eine (oder mehrere) Federkonstanten beschrieben werden kann.
Zur Analyse damit aufgebauter Systeme benötigt man auch noch Knoten- und Maschengleichungen:
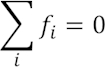
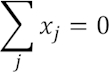
Knoten bestehen immer dort, wo sich Kraftflüsse aufteilen, also beispielsweise die Gewichtskraft einer Platte auf mehrere Standfüße „weitergeleitet“ wird. Eine Masche ist als sequentiell in einem System angeordnete Folge von Abständen zu sehen, die insgesamt eine geschlossene „Kurve“ ergeben, der Anfang dieser Kurve also mit dem Ende übereinstimmt.
WENN SIE ES GENAUER WISSEN WOLLEN: