WENN SIE ES GENAUER WISSEN WOLLEN:

Das Systemverhalten technischer Prozesse kann entweder durch eine Simulation analysiert werden oder auch auf Basis einer mathematischen Systembeschreibung. Für letztere geht man von linearen bzw. zumindest linearisierten Teilprozessen aus, woraus sich eine lineare Differentialgleichung generieren lässt, die das System bzgl. einer jeweils betrachteten Eingangs- und Ausgangsgröße beschreibt. Die Berechnung der Systemantworten zu relevanten Eingangssignalen erfordert zunächst das Lösen einer solchen Differentialgleichung, was bereits bei kleinen Systemen recht anspruchsvoll und zeitaufwendig ist. In diesem Kapitel wird deshalb ein alternatives Rechenverfahren auf Basis der sog. Laplace-Transformation hierfür angeboten. Es ist insbesondere in der Regelungstechnik auch stark verbreitet. Was sich auf den ersten Blick sehr abstrakt anhört, ist in seiner praktischen Anwendung – zumindest was das Lösen linearer Differentialgleichungen betrifft – relativ einfach. Und trotz eines „Umwegs“ im Rechengang deutlich schneller durchzuführen.
Die Grundidee
Statt die Differentialgleichung mit ihren beiden zeitabhängigen Größen direkt im sog. „Zeitbereich“ zu lösen, transformieren wir das Eingangssignal xe(t) in den sog. „Spektralbereich“ nach den Gesetzen der Laplace-Transformation. Wir erhalten formal ein Spektrum Xe(s) mit s als einer komplexen Frequenz. Wie wir nachfolgend ebenfalls noch sehen werden, kann man aus der Differentialgleichung sehr einfach eine Systemübertragungsfunktion F(s) ableiten, mit der wir Xe(s) nur multiplizieren müssen, um das zugehörige Ausgangsspektrum Xa(s) zu bestimmen. In einem letzten Schritt transformieren wir dieses wieder in den Zeitbereich zurück und erhalten das gesuchte Ausgangssignal xa(t).
Systemübertragungsfunktion
Im Zeitbereich gilt gemäß unseren Ausführungen im letzten Kapitel für den Zusammenhang zwischen Ein- und Ausgangssignal eine lineare Differentialgleichung. Transformiert man diese Gleichung mit Hilfe der Rechenregeln der laplace-Transformation in den Spektralbereich, so erhält man:
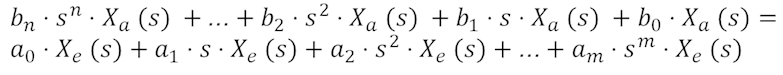
Statt Ableitungen kommen darin nur noch Multiplikationen mit s vor. n-mal Ableiten entspricht der Multiplikation mit sn. Dies lässt sich nun auflösen zu
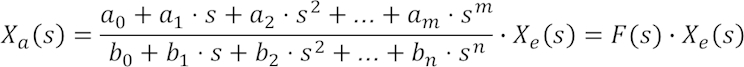
F(s) ist dabei die Systemübertragungsfunktion, formal eine komplexe Funktion über der komplexen Frequenz s, was uns für unsere Rechnungen aber meist nicht weiter kümmert. Interessant dabei ist, dass für jedes auch noch so umfangreiche lineare System mit vielen Elementen F(s) sehr einfach angebbar ist. Um ein Ausgangssignal für ein gegebenes Eingangssignal zu berechnen, müssen wir also statt des Lösens einer Differentialgleichung nur noch eine Multiplikation mit F(s) vornehmen und das Ergebnis abschließend in den Zeitbereich zurücktransformieren.
Berechnung von Systemantworten am Beispiel
Beispielhaft wollen wir für ein RC-Glied die Sprungantwort per Laplace-Transformation berechnen (was im Buch deutlich ausführlicher dargelegt wird, auch mit anderen Beispielen).
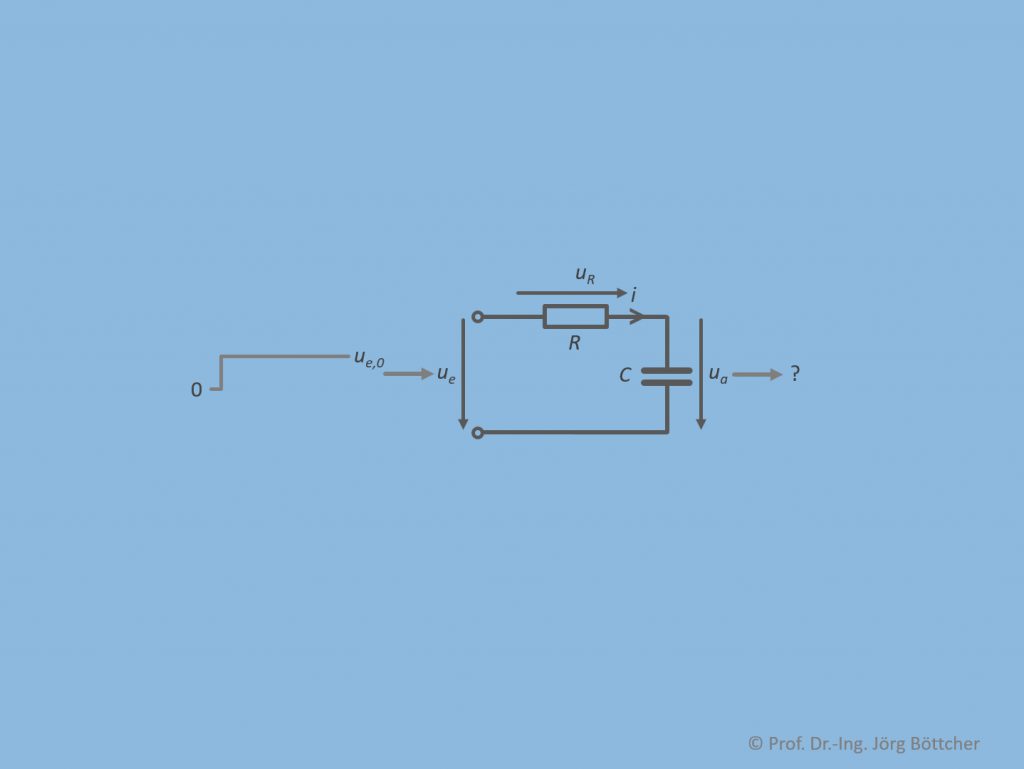
Berechnung der Sprungantwort für ein RC-Glied
Die Systemdifferentialgleichung für dieses System lautet
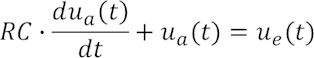
bzw. im Spektralbereich
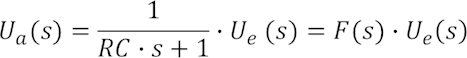
Mit der spektralen Schreibweise der Sprungfunktion für Ue(s) ergibt sich:
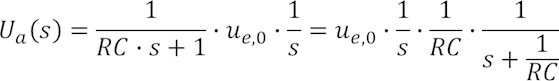
Damit haben wir nun die Basis für die Rücktransformation gelegt und können ansetzen:
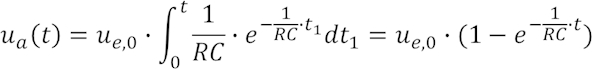
Das Ergebnis stellt eine Funktion dar, die beginnend bei 0 sich exponentiell dem Endwert ue,0 annähert. RC ist die hierbei relevante Zeitkonstante, nach deren Ablauf die Funktion sich auf ca. 63 % des Endwerts befindet. Nach zwei Zeitkonstanten hat man ca. 86 %, nach drei ca. 95 % und nach fünf schließlich über 99 % des Endwerts erreicht.
WENN SIE ES GENAUER WISSEN WOLLEN: