WENN SIE ES GENAUER WISSEN WOLLEN:
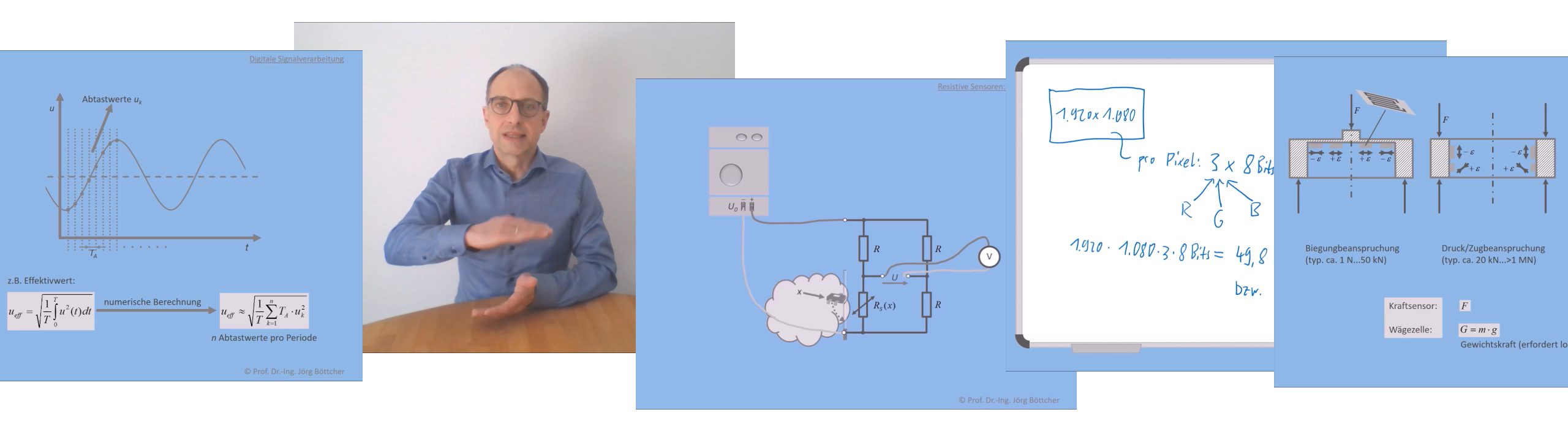
Soll bzw. kann ein technischer Prozess nicht in geschlossener mathematischer Darstellung beschrieben werden, was wir im letzten Kapitel mittels der Laplace-Transformation zumindest für sog. lineare Systeme noch durchführen konnten, so kann er in aller Regel dennoch simuliert werden. Simulationen lassen vielmehr Signale iterativ mit kleinsten simulierten Zeitabständen die Signalpfade zwischen den Elementarprozessen virtuell entlang laufen, wobei schritthaltend für jeden Elementarprozess dessen mathematische Beschreibung neu durchlaufen wird. Fast so, wie das auch im realen Prozess passiert, jedoch in kürzest möglicher Rechenzeit statt in Echtzeit. Viele mathematische Operationen in den Elementarprozessen werden in einem Schritt abgearbeitet und stellen kein größeres Problem bei der Realisierung von Simulationen dar. Anders sieht es jedoch mit den für Simulationen wichtigen Operationen des Differenzierens und Integrierens aus. Sie benötigen zur Berechnung immer auch die Vorgeschichte der Eingangsgröße. Da das Verständnis, wie man diese beiden Operationen numerisch implementiert, sehr wichtig ist, um die Arbeitsweise und Parametrierung von Simulationstools zu verstehen, wollen wir in diesem Kapitel näher darauf eingehen.
Numerisches Differenzieren
Simulationstools arbeiten zwangsweise nicht mit stetigen Analogsignalen, wie das reale technische Prozesse tun. Sie können vielmehr die Signale nur als Abtastwerte intern darstellen und verarbeiten, also in i.d.R. gleichbleibenden Zeitabständen den jeweiligen Signalwert zum sog. Abtastzeitpunkt wiedergeben. Vornehm ausgedrückt haben wir es mit zeitdiskreten Signalen zu tun. Auch die Signalwerte selbst sind bei genauer Betrachtung „gestückelt“, man spricht von Quantisierung. Dies hängt damit zusammen, dass ein Rechner Zahlenwerte nur in endlicher Auflösung speichern kann. Jedoch ist dies hinsichtlich der Simulationsgüte absolut vernachlässigbar und hat nichts mit der beschränkten Auflösung real abtastender Systeme über Analog-Digital-Umsetzer zu tun.
Wie kann man nun ein Signal programmgestützt differenzieren, wenn man nur über Abtastwerte verfügt? Zur Beantwortung erinnern wir uns daran, dass Differenzieren nichts anderes bedeutet als die Signaländerung über der Zeit. Verfügen wir nur über ein abgetastetes Signal x mit Abtastwerten zu ganzzahligen Vielfachen i einer Abtastzeit TA, so können wir die ideale stetige Differentiation annähern durch die Differenz eines Abtastwertes mit seinem Vorgänger, welche auf TA zu beziehen ist:
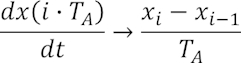
Je kleiner TA gewählt werden kann, umso mehr nähert sich die numerische Lösung dem stetigen Original an.
Das nachfolgende Bild zeigt ein abgetastetes Signal sowie dessen so berechnete Ableitung als Screenshots eines hierzu geschriebenen kleinen LabVIEW-Programms. Beide Graphen wurden dabei im zugehörigen Eigenschaftenmenü so konfiguriert, dass die eigentlichen Abtastwerte als Punkte dargestellt werden, die durch waagrechte Linien miteinander verbunden sind. Die so generierten Treppenkurven entsprechen den Signalverläufen, die man erhält, wenn man Abtastwerte über Digital-Analog-Umsetzer in entsprechenden Prozessmodulen als reale z.B. Spannungssignale ausgibt.
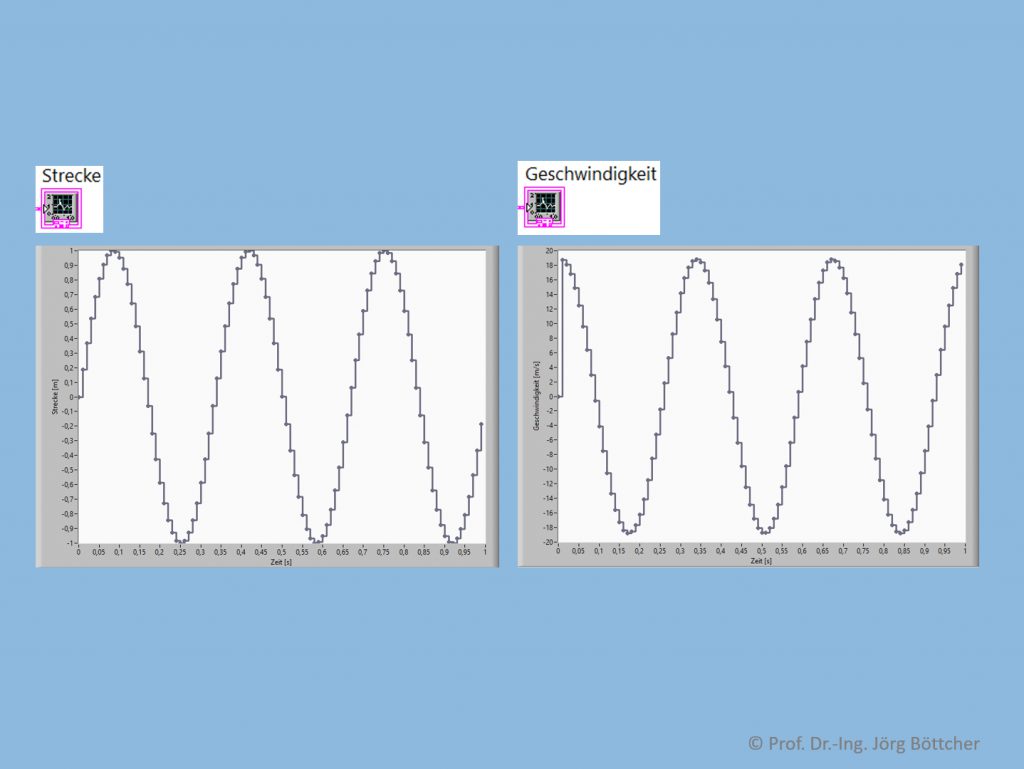
Originalabtastsignal „Strecke“ und numerisch differenziertes Abtastsignal „Geschwindigkeit“
Programmatisches Differenzieren in LabVIEW
Da einfache Simulationen oder davon unabhängig auch etwaige Signalverarbeitungsalgorithmen relativ einfach selbst programmiert werden können, wollen wir in unterem Bild das oben angesprochene kleine LabVIEW-Programm betrachten, das nach der Erzeugung einer Abtastfolge zu einem virtuell angenommenen Signal die Ableitung in allen Abtastwerten berechnet.
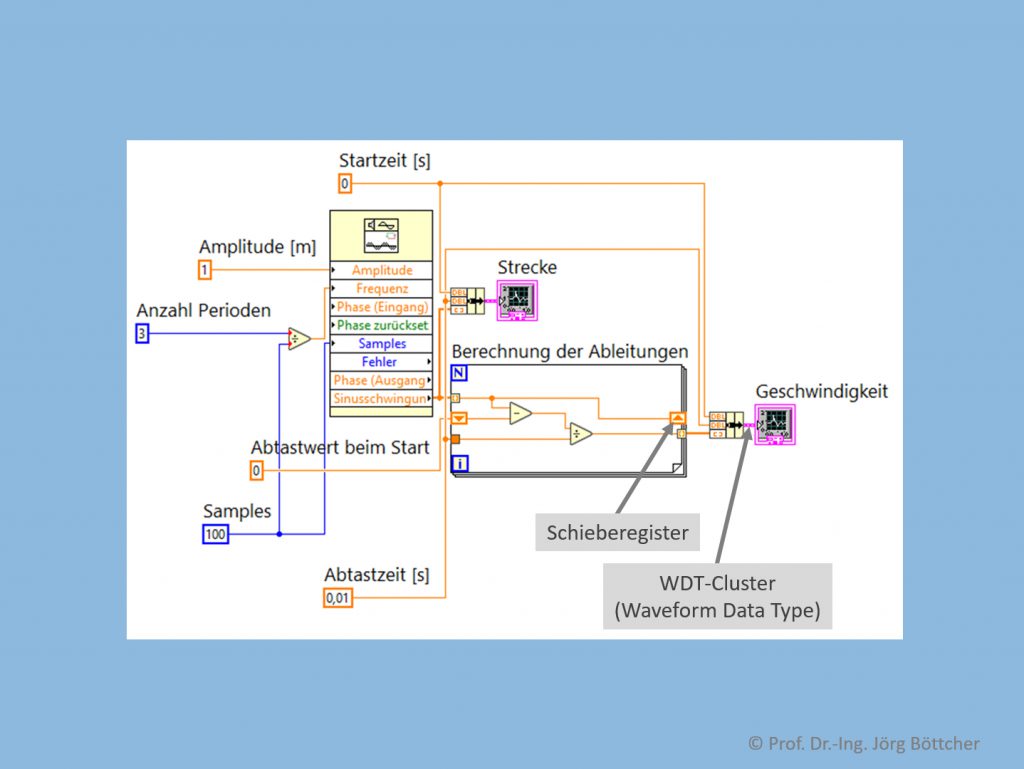
Numerisches Differenzieren in LabVIEW
Der mehr links angeordnete größere Funktionsblock stellt eine LabVIEW-Funktion dar, die auf Basis entsprechender Parameter an den Eingängen Abtastwerte einer Sinusfunktion berechnet und am Ausgang – beschriftet mit „Sinusschwingung“ – in einem numerischen Array ablegt. In unserem Beispiel werden 100 Abtastwerte („Samples“) berechnet. Arrays werden im Blockdiagramm zu LabVIEW-Programmen durch eine dicke Linie gekennzeichnet. Dieser Funktionsblock verwendet die Signalparameter nur zur internen Berechnung. Die ebenfalls zu parametrierende „Frequenz“ ist hierbei nicht in der Einheit Hertz (Hz) anzugeben, sondern als Anzahl von Perioden bezogen auf die angegebene Anzahl an Abtastwerten. Das Array wird also in schnellstmöglicher Rechenzeit mit den Abtastwerten befüllt.
Die eigentliche Differentiation findet in der For-Schleife (Rechteck in der Mitte des Bildes) statt. Diese Schleife so häufig widerholt, wie es Abtastwerte im Array gibt, wobei bei jedem Schleifendurchlauf ein neuer Abtastwert aus dem Array ins Schleifeninnere zur weiteren Verarbeitung übergeben wird. Im Schleifenkörper wird obige Formel nachgebildet und der jeweils berechnete Wert am rechten Schleifenrand nach außen übergeben.
Da zur Differenzbildung hierbei auf den Abtastwert des vorherigen Schleifendurchlaufs zurückgegriffen werden muss, muss man sich diesen merken. Dies geschieht bei LabVIEW vorteilhaft durch ein Schieberegister, das einen an sein Ausgangssymbol (Dreieck nach oben) geleiteten Wert im nächsten Schleifendurchlauf am zugehörigen Eingangssymbol (Dreieck nach unten) wieder einspeist. Für den ersten Schleifendurchlauf muss dieser von außen vorbelegt werden, was im Bild mit dem Wert 0 erfolgt.
Statt der selbst programmierten Schleife könnte man auch eine fertige Differenzierungsfunktion in LabVIEW einsetzen, wie sie nachfolgendes Bild mit Funktionssymbol (links) und Anschlussbeschreibung (rechts, Auszug aus der Onlinehilfe hierzu) zeigt. Gegenüber der oben vorgestellten einfachsten Differenzierungsmethode („Rückwärts“ genannt) lassen sich hierbei auch alternative Arten noch parametrieren.
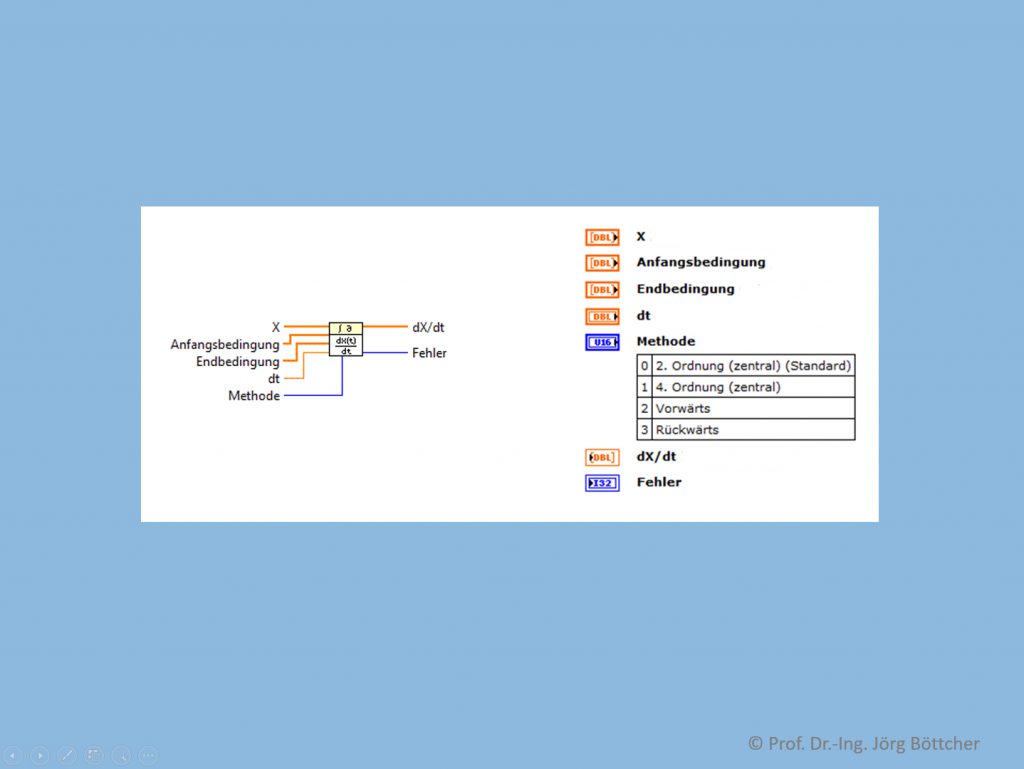
Differenzierungsfunktion in LabVIEW
Numerisches Integrieren
Integrieren bedeutet bei stetigen Signalen die Berechnung der Fläche unter der Kurve. Im Falle von abgetasteten Signalen können wir uns diese Fläche näherungsweise vorstellen als Summe von Rechteckflächen, wobei jedes Rechteck die Breite der Abtastzeit TA aufweist, während seine Höhe dem jüngsten Abtastwert entspricht. Mathematisch formuliert ergibt dies:
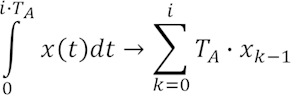
Die Formel bedeutet, dass wir beginnend mit dem ersten Abtastwert aufsummieren müssen. In der Formel haben wir dabei als Index des jeweiligen Abtastwertes k-1 geschrieben, da wir davon ausgegangen sind, dass ein Rechteck erst dann mit seiner Fläche einfließen soll, wenn man auf der Zeitachse an seinem rechten Rand angekommen ist. Der Abtastwert zum Index -1 ist dabei als 0 anzunehmen. Man könnte natürlich auch zu einem Abtastzeitpunkt gleich das hierzu gehörige neue Rechteck aufsummieren und als Index dann k schreiben (wie dies in vielen anderen Veröffentlichungen auch gemacht ist). Auch hier gilt wieder, dass ein kleineres TA zu einer besseren Approximation des stetigen Integrals führt.
Obige Formel kann man selbst programmiertechnisch umsetzen oder z.B. in LabVIEW fertige Integrationsfunktionen verwenden.
WENN SIE ES GENAUER WISSEN WOLLEN: