EIN
KOMPAKTER ÜBERBLICK

Wir beschäftigen uns in diesem Überblick zunächst mit grundsätzlichen Ausführungsformen von Sensoren – vom Sensorelement bis zum installationsfertigen Sensor mit Digitalschnittstelle. Danach geht es um grundsätzliche Anordnungen zur Auswertung der Signale resistiver, induktiver und kapazitiver Sensoren. Neben vielen anderen Schaltungen spielt hier insbesondere die Brückenschaltung eine große Rolle.
Ausführungsformen von Sensoren
Der Begriff Sensor – auch als „Messaufnehmer“ oder schlicht „Aufnehmer“ bezeichnet – bezieht sich auf eine Komponente, die eine nichtelektrische Messgröße in ein elektrisches Primärsignal umwandelt, das dann mit weiteren Elektroniken weiterverarbeitet werden kann. Bei einigen Messgrößen hat sich der zugehörige Sensormarkt dabei aufgeteilt: Der eigentliche physikalische (mitunter auch chemische) Prozess, der für die Generierung des elektrischen Primärsignals zuständig ist, wird in Form eines meist relativ kompakten Bauelements ausgeführt. Dieses ist oftmals, jedoch nicht immer, so gebaut, dass es direkt auf elektronischen Leiterplatten montiert werden kann. Den Herstellern derartiger Sensorelemente stehen Hersteller gegenüber, die diese dann mit anwendungsspezifischen Gehäusen versehen, Auswerteelektroniken integrieren, Kabel bzw. Anschlussklemmen ergänzen etc. Sie produzieren installationsfertige Sensoren. Im Wesentlichen kommen heute folgende Fertigungstechnologien bei der Herstellung von Sensorelementen zur Anwendung:
- Feinmechanik
- Spritzgießen
- Schweißen
- Mikrotechnologien
Die Mikrotechnologien sind seit einigen Jahren so weit entwickelt, dass sich damit auf einem Chip nicht nur die reine Sensorfunktion realisieren lässt. Vielmehr werden zusätzlich hochintegrierte analoge und digitale Elektroniken integriert. Als Fachbegriff für derartige Chips hat sich MEMS (Micro Electro Mechanical System) herausgebildet.
Der starke Trend in allen Branchen geht zu installationsfertigen Sensoren mit Digitalschnittstelle. Deren internen Aufbau zeigt das Bild.
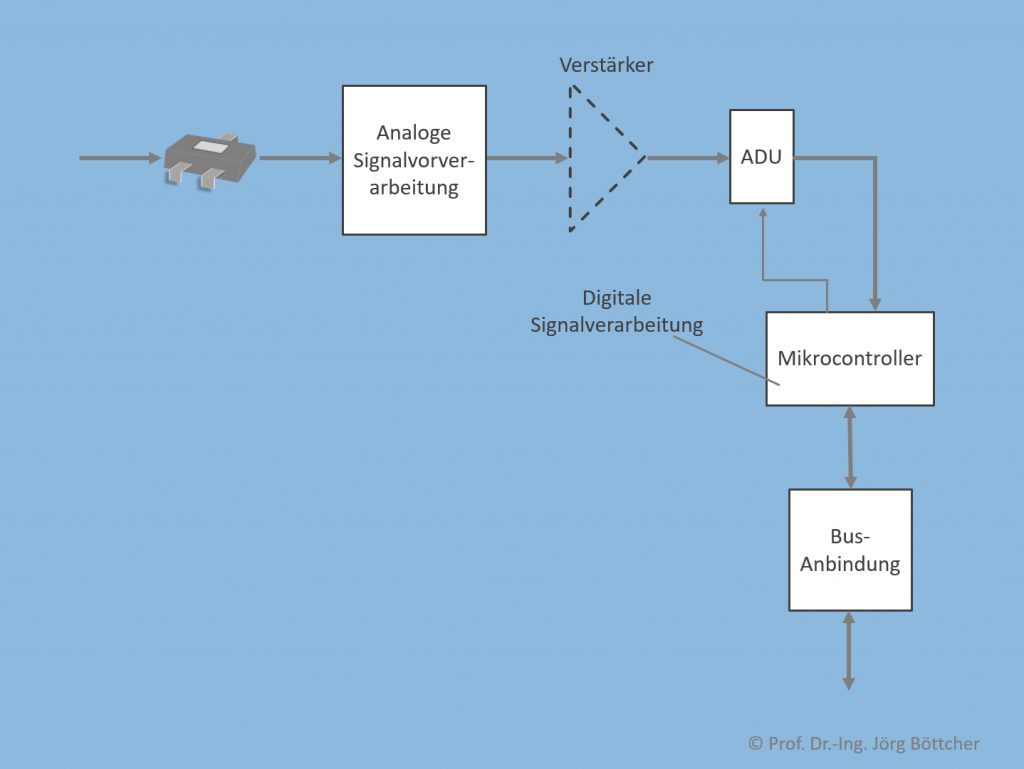
Interner Aufbau eines Sensors mit Digitalschnittstelle
Auswertung resistiver Sensoren
Resistive Sensoren werden über eine Messung ihres ohmschen Widerstands ausgewertet, was zunächst über die separate Messung von Spannung und Strom und deren anschließende Verrechnung über das ohmsche Gesetz erfolgen kann. Je nach der Reihenfolge, wie Spannungs- und Strommesseingänge an den Sensor verschaltet werden, spricht man von stromrichtiger bzw. spannungsrichtiger Verschaltung. Bei ersterer erhält man einen um den Innenwiderstand des Strommesseingangs RA erhöhten Wert. Bei letzterer einen um einen gewissen Faktor, in dem der Innenwiderstand des Spannungsmesseingangs RV enthalten ist, zu niedrigen Wert. Beides kann durch Berücksichtigung des jeweiligen Innenwiderstandes systematisch korrigiert werden.
Möchte man keinen Strommesseingang verwenden, so lässt sich die Widerstandsbestimmung auch auf zwei Spannungsmessungen zurückführen, insofern man einen bekannten Referenzwiderstand in Serie zum resistiven Sensor schaltet. Das Verhältnis der an beiden Widerständen zu messenden Spannungen entspricht dem Verhältnis der zwei Widerstände, woraus der Sensorwiderstand ermittelt werden kann. Auch hier kann man die Innenwiderstände der Spannungsmesseingänge zur Erzielung einer höheren Genauigkeit durch eine Korrekturrechnung kompensieren.
Resistive Sensoren müssen mitunter vom Ort ihrer Installation bis zur Messelektronik über ein längeres Kabel verdrahtet werden. Der Kabelwiderstand würde hier zunächst mitgemessen. Die Korrektur dieses Kabelwiderstands ist einfach, wenn man ihn einmalig bestimmt, was durch Messung am installierten Kabel oder durch Berechnung auf Basis der verlegten Kabellänge und den Kabeldaten laut Datenblatt geschehen kann. Beides ist in der Praxis jedoch mitunter zeitaufwendig und fehleranfällig, weshalb sich eine nur geringfügig teurere schaltungstechnische Alternative, die Vierleitertechnik gemäß nachfolgendem Bild durchgesetzt hat. Da im Spannungsmesskreis angesichts des üblicherweise sehr hohen Innenwiderstands eines Spannungsmesseingangs praktisch kein Strom fließt, entsteht über die Leitungslänge der zugehörigen Leiter im Kabel auch keine zusätzliche Spannung. Der Spannungsmesseingang „sieht“ trotz des langen Kabels die Spannung direkt am Sensor.
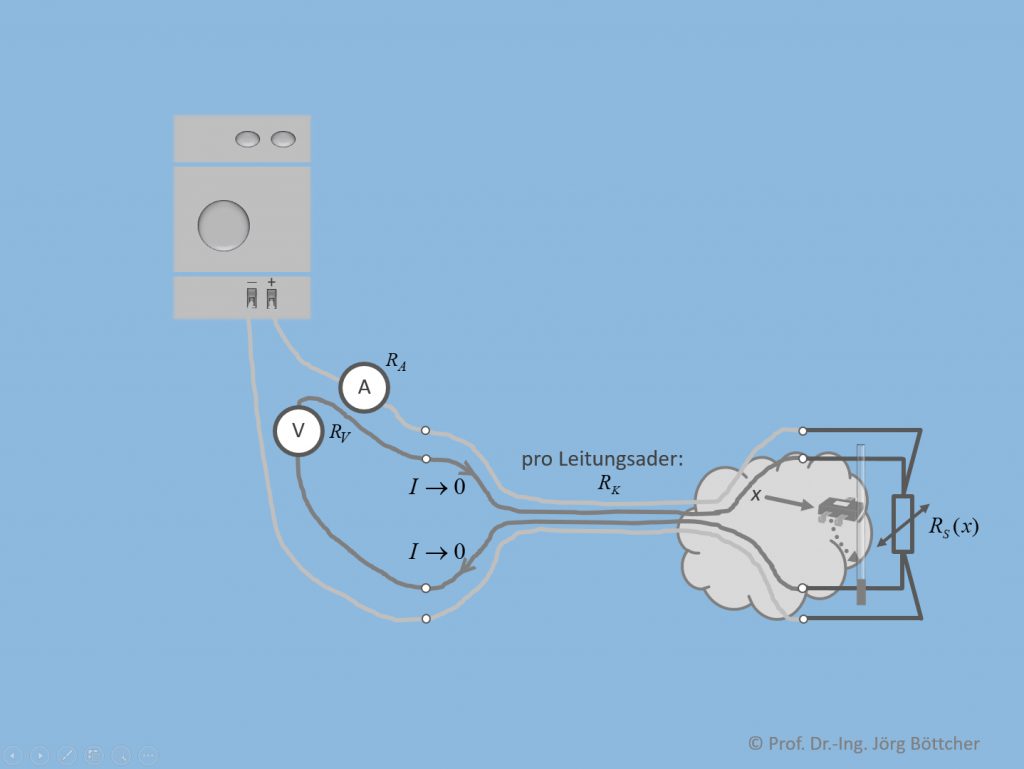
Vierleitertechnik
Brückenschaltungen für resistive Sensoren
Die einfachste Variante einer Brückenschaltung stellt die Viertelbrücke gemäß unterem Bild dar. Von den insgesamt vier Widerständen ist einer (also ein Viertel aller vier) veränderlich und zwar der resistive Sensor, dessen Widerstand RS sich in Abhängigkeit der Messgröße x ändert. Die anderen drei Widerstände R sind Festwiderstände. Die Schaltung wird durch eine Gleichspannung U0 gespeist und erzeugt an ihrem Ausgang eine Spannung U (auch „Brückenspannung“ oder „Diagonalspannung“ genannt).
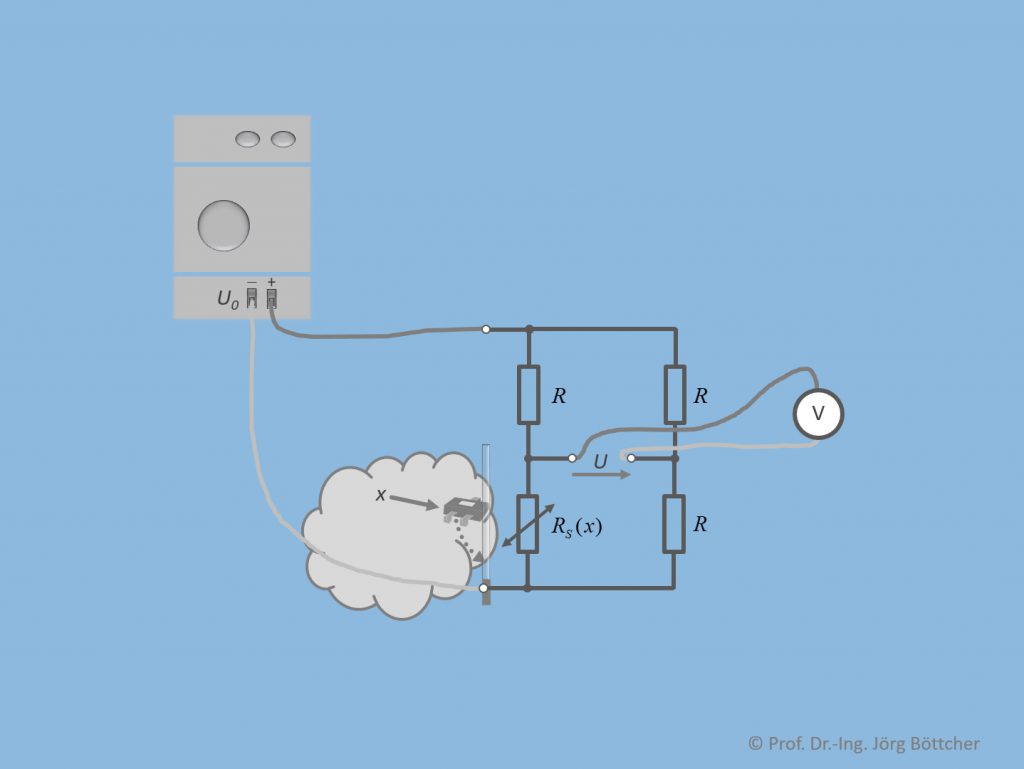
Viertelbrücke
Zum Verständnis von Brückenschaltungen muss man sich RS stets zusammengesetzt denken aus einem Grundwert R, den der Sensor ohne Anlegen der Messgröße, also bei x = 0 aufweist, und einem durch die Messgröße bewirkten Messeffekt ΔR(x):
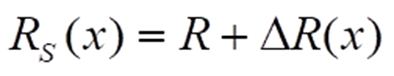
Die Brücke selbst wandelt diesen Messeffekt unter der Voraussetzung einer bei vielen (aber nicht allen) Sensoren kleinen Signaländerung
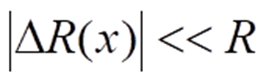
um in eine näherungsweise dazu proportionale Ausgangsspannung
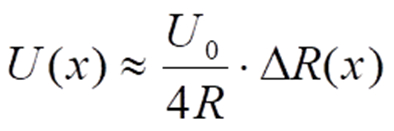
Hierbei ist wichtig, dass die Festwiderstände der Brücke dem Grundwert R des Sensors entsprechen.
Bei ausgewählten Sensorinstallationen bzw. vereinzelt auch bei sensorinternen Konstruktionsstrukturen ist es möglich, zwei baugleiche Sensoren zu verwenden, die von einer Messgröße x in genau entgegengesetzter Richtung ausgesteuert werden. Diese können unter Verwendung von jetzt nur noch zwei weiteren Festwiderständen zu einer sog. Halbbrücke verschaltet werden. Vorteile sind dabei eine exakt lineare Funktion der Brücke selbst, eine doppelt so große Ausgangsspannung und eine hochwertige Kompensation von auf beide Sensoren gleichermaßen wirkenden Störgrößen.
In der messtechnischen Praxis gibt es einen Sensortyp, der meist in einer noch weitergehenden Brückenschaltung verschaltet wird: der Dehnungsmessstreifen. Dieser liefert so kleine Messeffekte, dass er eine gegenüber der Halbbrücke nochmals verdoppelte Ausgangsspannung gut „vertragen“ kann, zumal er als zunächst eher einfaches Sensorelement vergleichsweise preisgünstig ist. Bei der entsprechenden Brückenschaltung handelt es sich um eine Vollbrücke mit vier Sensoren und ohne zusätzliche Festwiderstände.
Auswertung kapazitiver und induktiver Sensoren
Kapazitive und induktive Sensoren können mit denselben Messverfahren, wie wir sie bislang zu den resistiven Sensoren beschrieben haben, ausgewertet werden. Wir müssen lediglich mit Wechselspannungen arbeiten und, insofern die Schaltungen bislang Festwiederstände vorsahen, diese zumindest teilweise durch Kondensatoren bzw. Induktivitäten festen Werts ersetzen. Mitunter finden sich auch alternative, fest in die Sensoren integrierte Auswerteelektroniken, bei denen die zu messenden Sensoren frequenzbestimmender Teil einer Oszillatorschaltung sind, womit ein frequenzmoduliertes Ausgangssignal erzeugt wird. Die Frequenzmessung soll hier nicht weiter betrachtet werden; sie wird in einem anderen Teil behandelt.
Die sog. Blindwiderstände von Kapazitäten bzw. Induktivitäten sind
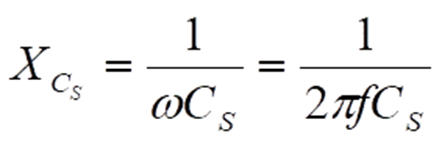
bzw.
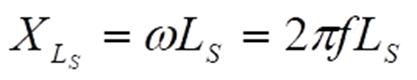
Durch Messung von Wechselstrom und Wechselspannung bevorzugt nach ihren Effektivwerten lässt sich folglich hierüber Cs bzw. Ls ermitteln. Im Unterschied zur Auswertung bei resistiven Sensoren benötigen wir zusätzlich noch die Kreisfrequenz des zur Versorgung verwendeten Sinussignals. Speziell induktive Sensoren weisen in der zur Realisierung einer Induktivität zwangsweise benötigten Spulenwicklung einen gewissen ohmschen Verlustwiderstand auf. In diesem Fall gilt die analoge Anwendung des ohmschen Gesetzes für Blindwiderstände nicht mehr ganz exakt. Wir können diesen Effekt jedoch bei Kenntnis des ohmschen Wicklungswiderstandes RW durch eine entsprechende Korrekturrechnung eliminieren.
Ebenfalls möglich ist eine Messung über ein Referenzelement. Das Referenzelement muss vom gleichen Typ sein: bei einem kapazitiven Sensor also ein Festkondensator, bei einem induktiven Sensor eine Spule festen Werts.
Brückenschaltungen für kapazitive und induktive Sensoren
Auch bei kapazitiven bzw. induktiven Sensoren ist es möglich, mittels Brückenschaltungen ausschließlich den Messeffekt an sich in eine entsprechende Ausgangsspannung umzuwandeln. Das untere Bild zeigt hierzu zunächst eine Viertelbrücke.
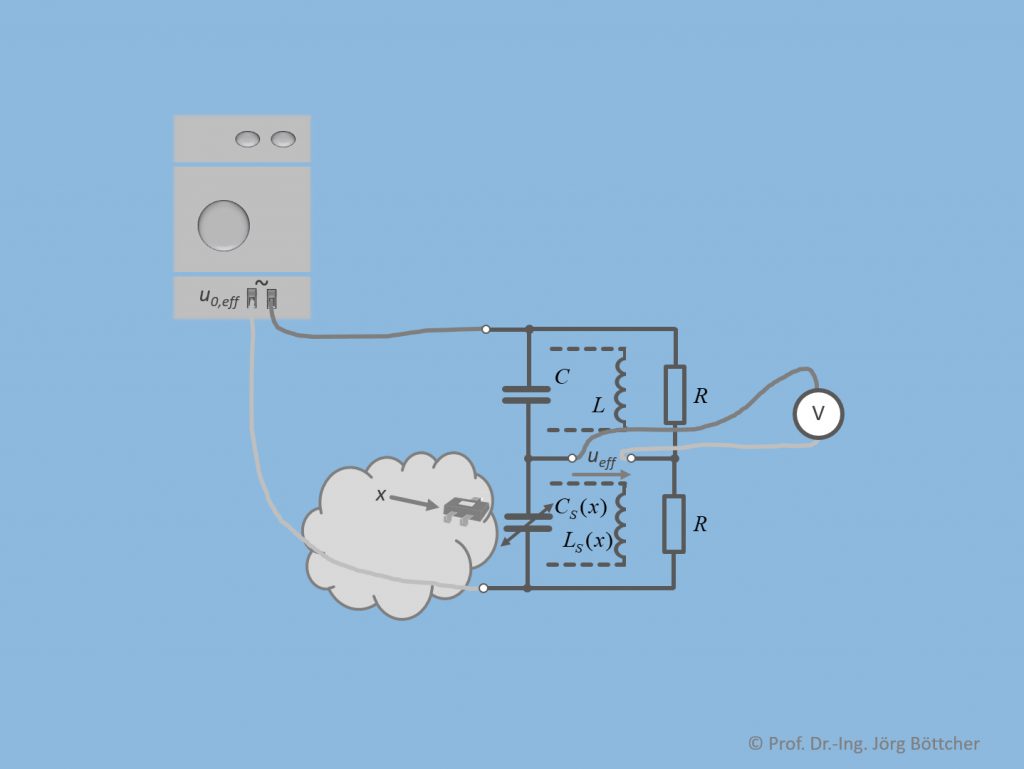
Viertelbrücke für kapazitive bzw. induktive Sensoren
Der Betrieb mit Wechselspannung bringt es mit sich, dass die Information über das Vorzeichen von des Messeffekts verloren geht. Wird dieses von der Anwendung her jedoch benötigt, so kann es beispielsweise aus der Phasenverschiebung des Ausgangssinussignals bezogen auf das Sinussignal der Versorgungsspannung detektiert werden. Die Phasenauswertung übernehmen z.B. sog. phasenselektive Wechselspannungsverstärker.
Auch bei kapazitiven und induktiven Sensoren sind Halbbrücken vorteilhaft, sofern von der Anordnung her zwei entgegengesetzt wirkende Blindwiderstandsänderungen generiert werden können. Vollbrücken sind bei kapazitiven und induktiven Sensoren nicht verbreitet. Auch die bei resistiven Sensoren besprochene Vierleitertechnik findet sich hier nicht. Der Grund liegt darin, dass ein auch nur etwas längeres Kabel bereits signifikante Kapazitäts- und Induktivitätsbeläge aufweist, die zusätzlich zu den sensoreigenen Blindwiderständen auch im Spannungsmesskreis wirken und zu deutlichen Messabweichungen führen würden. Längere Kabel zwischen Sensor und Messelektronik sind bei kapazitiven und induktiven Sensoren generell zu vermeiden.
WENN SIE ES GENAUER WISSEN WOLLEN: