EIN
KOMPAKTER ÜBERBLICK
In diesem Beitrag geht es um zwei wichtige Labormessgeräte: Das Oszilloskop stellt periodische sowie einmalige Spannungssignale über der Zeit dar. Der Spektrumanalysator wertet dagegen die in einem über eine gewisse Messzeit anliegenden Spannungssignal enthaltenen Frequenzanteile, das sog. Spektrum, aus. Obwohl beide Gerätearten zunächst nur elektrische Spannungen messen können, lassen sich alle anderen messtechnischen Größen ebenfalls damit darstellen, insofern sie in elektrische Spannungen umgeformt werden. Insbesondere bei von Sensoren generierten Signalen ist dies interessant.
Oszilloskop
Ein Oszilloskop kann i.d.R. bis max. acht Spannungssignale im Display anzeigen. Die X-Achse stellt im Normalbetrieb die verstrichene Zeit dar (siehe Bild). Die vergangene Zeit zwischen zwei hierzu im Display eingeblendeten senkrechten Hilfslinien (sog. Division, div) kann in einem weiten Bereich eingestellt werden. Man spricht hierbei von der horizontalen Empfindlichkeit bzw. dem horizontalen Ablenkkoeffizienten. Ebensolches gilt für die Y-Achse, die bzgl. der Spannungsdarstellung skaliert werden kann. Hiermit zusammen hängen auch die Einstellungen des Anfangs der Signaldarstellung in horizontaler Position (t = 0) und der Nulllinie (Ground GND). Für den Signalbeginn bei t = 0 wird eine sog. Triggerbedingung bezogen auf das darzustellende Signal definiert. Die im Display links gezeigten Signalverläufe vor diesem Zeitpunkt stellen somit die Vergangenheit dar. Letzteres ist möglich, da das Oszilloskop kontinuierlich die Signale einliest und dabei immer eine gewisse Signalhistorie speichert.
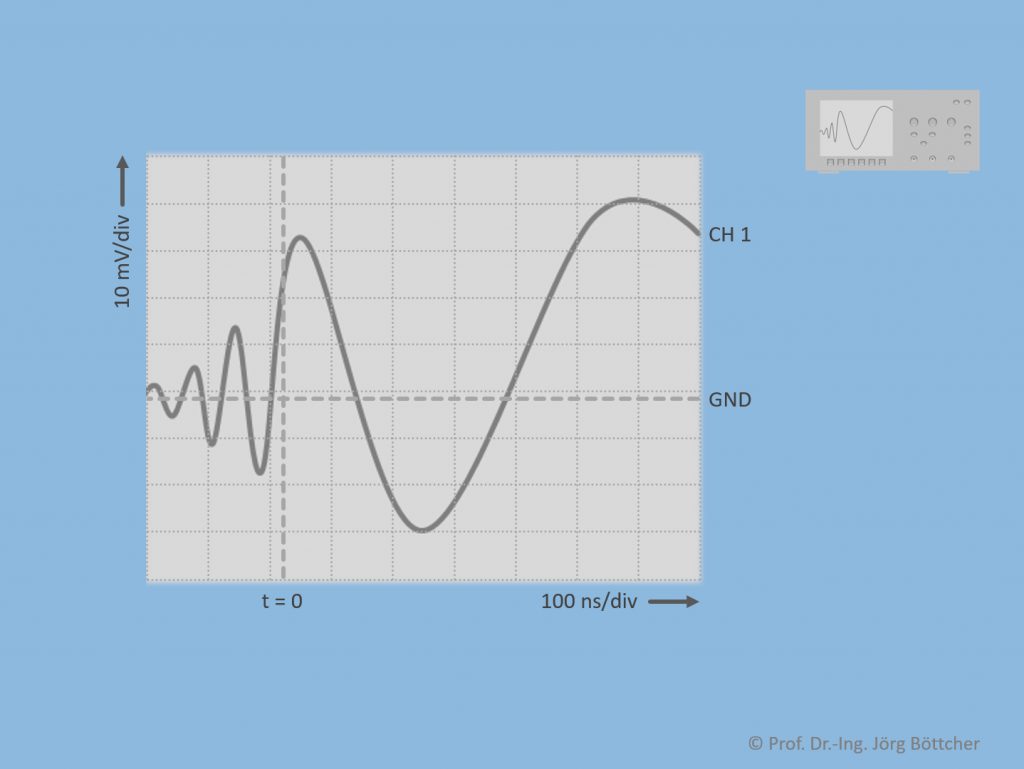
Spannungssignal über der Zeit im Display des Oszilloskops
Für jedes Signal kann dabei die Art der Kopplung parametriert werden. Üblicherweise sind hierbei folgende Optionen möglich:
- DC: Direct Current, Signal wird unverändert dargestellt.
- AC: Alternate Current, vor der Darstellung wird der Signalgleichanteil (Mittelwert) heraus gefiltert.
- GND: Es werden für Testzwecke genau 0 V angelegt.
- Invertiert: Das Signal wird negiert.
- HF-Filter: Zur Unterdrückung höherfrequenter Störsignale kann ein Tiefpassfilter mit oftmals 20 MHz eingekoppelt werden.
- Tastkopf: Es wird ein externer Tastkopf verwendet, dessen Teilerfaktor bei der Darstellung im Display berücksichtig wird.
Während die ersten drei Optionen alternativ einstellbar sind, können die drei weiteren beliebig dazu kombiniert werden.
Triggerung
Die Triggerbedingung besteht im einfachsten (und auch mit Abstand am häufigsten verwendeten) Fall aus der Konfiguration eines Signalpegels und der Angabe, ob bei steigender oder fallender Signalflanke (engl. Slope) getriggert werden soll. Erst wenn das für die Triggerung verwendete Signal genau diese Bedingung erfüllt, wird mit der Signaldarstellung begonnen und zwar genau so, dass der Signalwert zum Triggerzeitpunkt an der Stelle t = 0 im Display aufgeführt wird. Der für die Triggerung zu verwendende Kanal wie auch hierfür anzuwendende Kopplungsarten können ebenso konfiguriert werden. Darüber hinaus bieten Oszilloskope i.d.R. auch komplexere Triggervarianten an wie z.B. Time Delay oder Impulsbreitentriggerung.
Betriebsmodi
Bei dem in obigem Bild gezeigten Display handelt es sich um den Ausschnitt eines sich wie auch immer weiter entwickelnden einmaligen Signals. Derartige Signalausschnitte werden im sog. Single Sweep Mode des Oszilloskops erfasst. Hierunter ist zu verstehen, dass das Display nach Erfüllung der Triggerbedingung genau einmal beschrieben wird.
Periodische Signale werden dagegen im „Continous Mode“ dargestellt. Das Gerät wartet nach einem Signalschrieb im Display erneut auf das Eintreffen der konfigurierten Triggerbedingung, um dann sofort eine neue Displaydarstellung durchzuführen. Die Signaldarstellung wird also kontinuierlich erneuert.
Je nach Gerät gibt es weitere Betriebsarten wie eine rollierende Darstellung oder den heute praktisch nicht mehr benutzten XY-Betrieb.
Kenndaten von Oszilloskopen
Nachfolgendes Bild gibt typische Kenndaten von Oszilloskopen wider. Oszilloskope sind heute in einem weiten Preisbereich von etwa 150 EUR bis zum Preis eines Automobils der Kompaktklasse erhältlich. Der wichtigste Wert zur Beurteilung der Leistungsfähigkeit eines Oszilloskops ist hierbei die Grenzfrequenz. Mit ihr korrelieren auch etliche andere Kenndaten.

Kenndaten von Oszilloskopen
Tastköpfe
Im praktischen Einsatz eines Oszilloskops befindet sich zwischen der eigentlichen Messstelle und dem Kanaleingang ein mehr oder weniger langes Kabel, dessen eigene elektrische Eigenschaften ebenso eine Signalverfälschung herbeiführen können. Genauer gesagt ist es die Kapazität zwischen den beiden Leitern des Kabels, die sich hier parallel zum Messeingang auswirkt. Aus diesem Grund wird bei der Messung von Signalen mit etwas höheren Frequenzen statt eines einfachen Kabels ein sog. Tastkopf zwischen Messstelle und Messeingang geschaltet.
Tastköpfe sind meist als sog. passive Tastköpfe ausgeführt. Sie schalten in den Signalpfad lediglich eine Parallelschaltung einer z.B. über einen kleinen Trimmstift einstellbaren Kapazität CT und eines festen Widerstands RT (siehe Bild). Das nachfolgende Kabel – typischerweise als fest am Tastkopf montiertes Koaxialkabel mit BNC-Stecker ausgeführt – habe eine Kabelkapazität von CK.
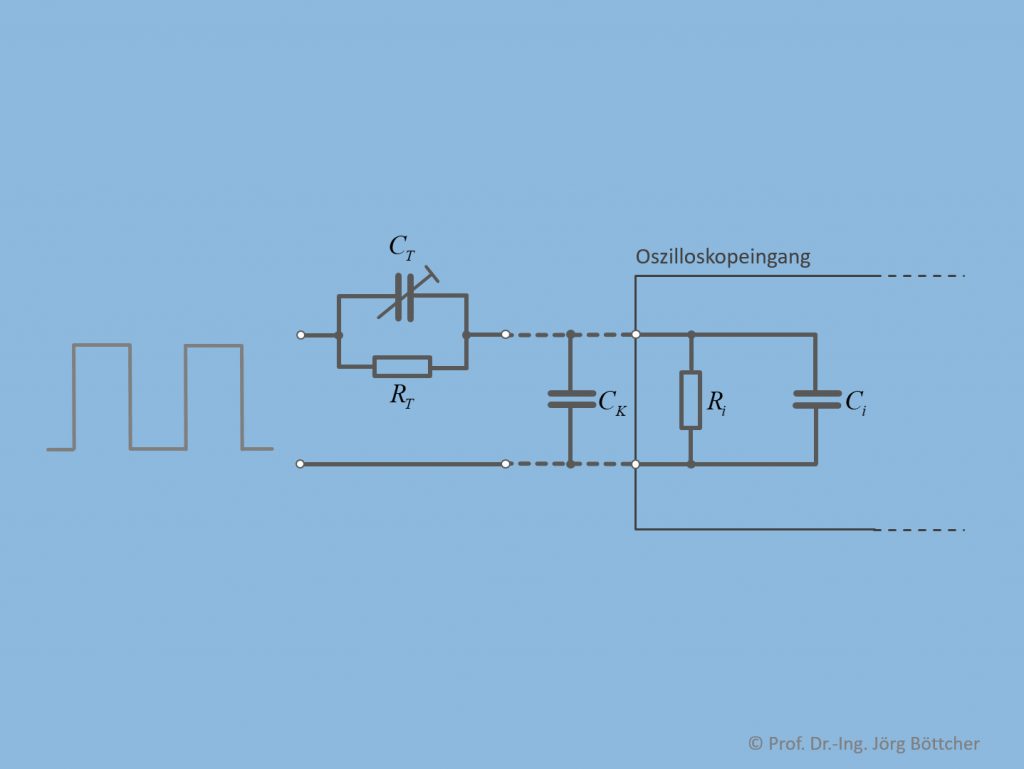
Passiver Tastkopf am Oszilloskopeingang
Betrachtet man die sich ergebenden Schaltungsverhältnisse zunächst rein auf Gleichspannungsbasis, so sieht man, dass durch RT und Ri ein Spannungsteiler entsteht, der die zu messende Spannung an der Tastkopfspitze um den Teilerfaktor
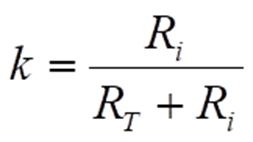
herabsetzt, weshalb ein Tastkopf auch als „Tastteiler“ bezeichnet wird. Im Falle einer Wechselspannung hängt der Teilerfaktor bedingt durch die beteiligten Kapazitäten jedoch von der Frequenz ab, was dazu führt, dass Signalformen entsprechend ihrer Frequenzanteile verfälscht werden. Man kann zeigen, dass bei einer bestimmten Einstellung von CT diese Frequenzabhängigkeit entfällt und Signale dann wieder korrekt dargestellt werden.
Spektrumanalysator
Im Unterschied zu einem Oszilloskop stellt ein Spektrumanalysator die Frequenzanteile eines kontinuierlich am Messeingang liegenden Signals dar. Die X-Achse stellt hierbei Frequenzwerte dar (siehe Bild). Auf der Y-Achse werden die Amplituden der einzelnen Frequenzanteile i.d.R. als Spannungspegel in der Einheit dBm angegeben.
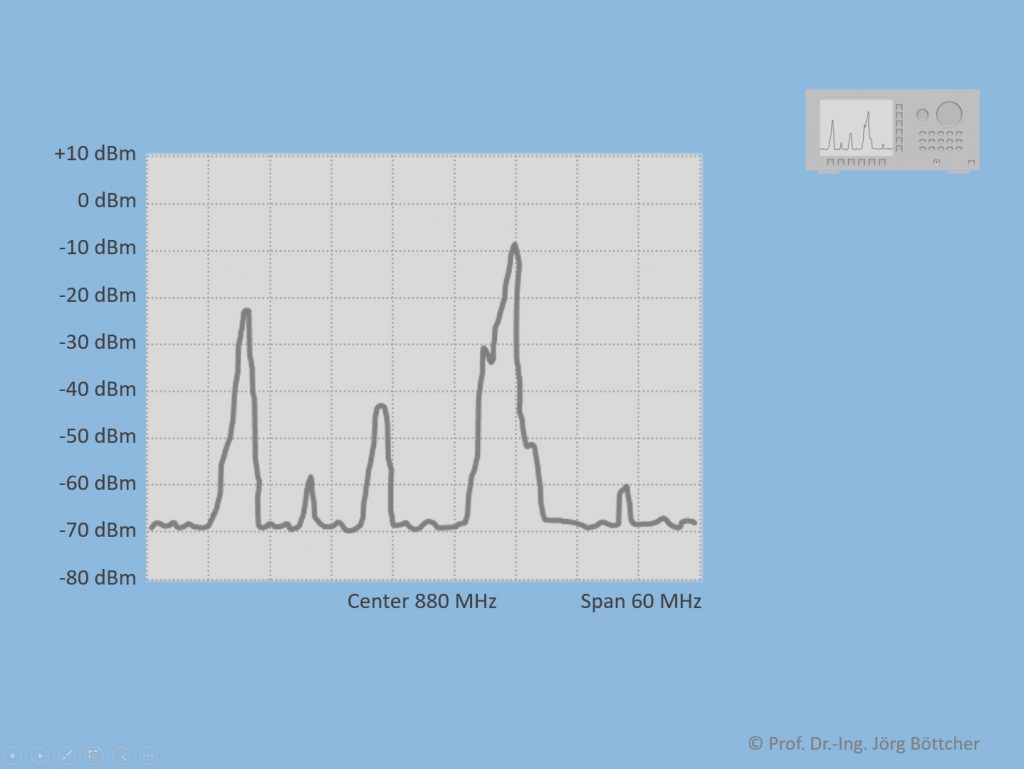
Spektrale Darstellung im Display des Spektrumanalysators
Frequenzanalyse über Zwischenfrequenz
Spektrumanalysatoren verfügen über eine anspruchsvolle Analogelektronik, die den Großteil des schaltungstechnischen Aufwands derartiger Geräte ausmacht. Deren Qualität entscheidet maßgeblich über die erzielbaren Kenndaten. Das zu messende Spannungssignal wird dabei zunächst an ein Tiefpassfilter geführt, das sicherstellt, dass keine Signalanteile mit Frequenzen oberhalb einer gerätespezifischen Maximalfrequenz fmax die nachfolgenden Stufen erreichen. Von zentraler Bedeutung für die Funktion ist die nach dem Tiefpass befindliche sog. Mischstufe. Diese ist nichts anderes als ein Multiplizierer, der das Signal nach und nach jeweils über eine gewisse Zeitdauer mit einem Sinussignal ansteigender Frequenz multipliziert. Dadurch wird systematisch ein jeweils neu gewählter kleiner Frequenzausschnitt des Signals in einen Bereich um eine feste Zwischenfrequenz fZF herum hochgesetzt.
Ein so in seiner Frequenz angehobener Frequenzausschnitt wird meist noch etwas verstärkt und dann durch ein relativ schmalbandiges Bandpassfilter geführt. Dieses weist als Mittenfrequenz (also der Frequenz, an der die maximale Durchlässigkeit besteht) genau fZF auf. Seine Aufgabe ist es, nur Signalanteile in diesem engen Frequenzbereich passieren zu lassen. Nachfolgend wird das übrig gebliebene Signal durch eine entsprechend schnelle digitale Schaltungselektronik mit bezogen auf fZF recht hoher Abtastrate abgetastet. Über eine digitale Signalverarbeitungsalgorithmik wird der Signalpegel nach gewissen Kriterien bestimmt und letztlich als Signalpegel über der ursprünglichen Signalfrequenz im Display angezeigt. Um dies an vielen Stellen über den gesamten Frequenzbereich durchzuführen, ist eine gewisse Messzeit, die sog. Sweep Time, notwendig.
Fourier-Reihe periodischer Signale
Um besser zu verstehen, was sich hinter dem Frequenzanteil der Messsignale eines Spektrumanalysators verbirgt, wollen wir ein wenig in die Theorie einsteigen: Jedes periodische Signal kann, wie uns die Mathematik sagt, als unendliche Summe elementarer Cosinus- und Sinusfunktionen mit Frequenzen von ganzzahligen Vielfachen der Grundfrequenz f0 des Signals beschrieben werden:
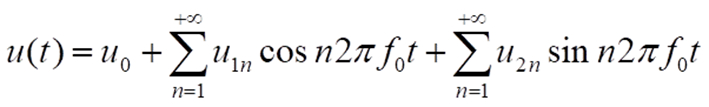
Dies ist die sog. Fourier-Reihe (oder auch Fourier-Zerlegung) eines periodischen Signals. u0 ist der Gleichanteil (Mittelwert) des Signals, der sich wie die Koeffizienten u1n und u2n signalspezifisch über entsprechende Formeln berechnen lassen.
Spektrum eines Rechtecksignals
Für ein gleichanteilsfreies, symmetrisches Rechtecksignal ergibt sich in Abhängigkeit von Amplitude und Frequenz beispielsweise nachfolgende Fourier-Reihe:
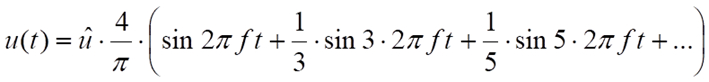
Für ein solches Summensignal mit 10 MHz Frequenz und 1 V Amplitude sind nachfolgend sowohl das zeitliche Signal als auch das Spektralbild aufgeführt, wenn man nur bis zur dritten sog. Oberwelle geht:
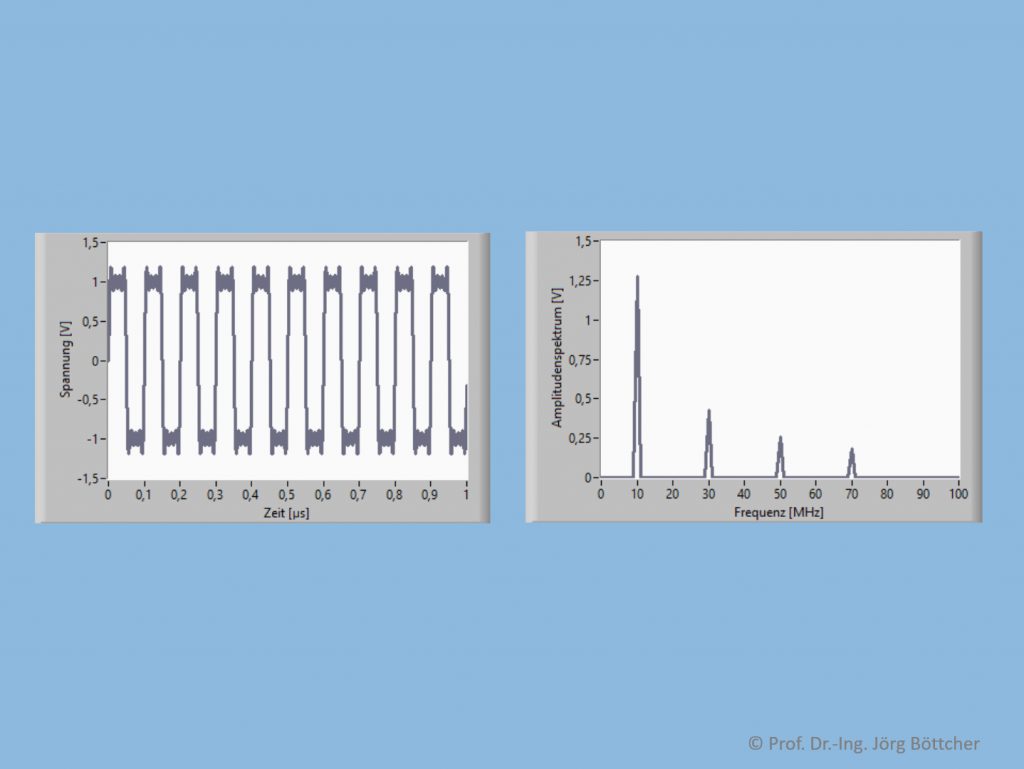
Rechtecksignal mit erster bis dritter Oberwelle sowie Spektrum
Weitere Beispielspektren
Wir wollen noch einige weitere Beispielspektren aufführen. So lautet die Fourier-Reihe für ein gleichanteilsfreies Dreiecksignal:
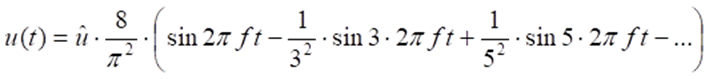
Ein Sägezahnsignal, eine in der Technik häufiger vorkommende Signalform, weist folgende spektrale Zerlegung auf:
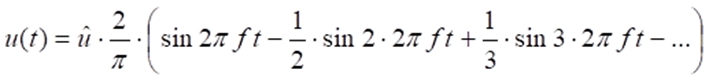
Unteres Bild zeigt schließlich noch das Spektralbild eines 10 MHz-Sinussignals mit 1 V Amplitude, dem jedoch ein sog. breitbandiges Rauschen überlagert ist, wie es in der Praxis stets vorkommt.
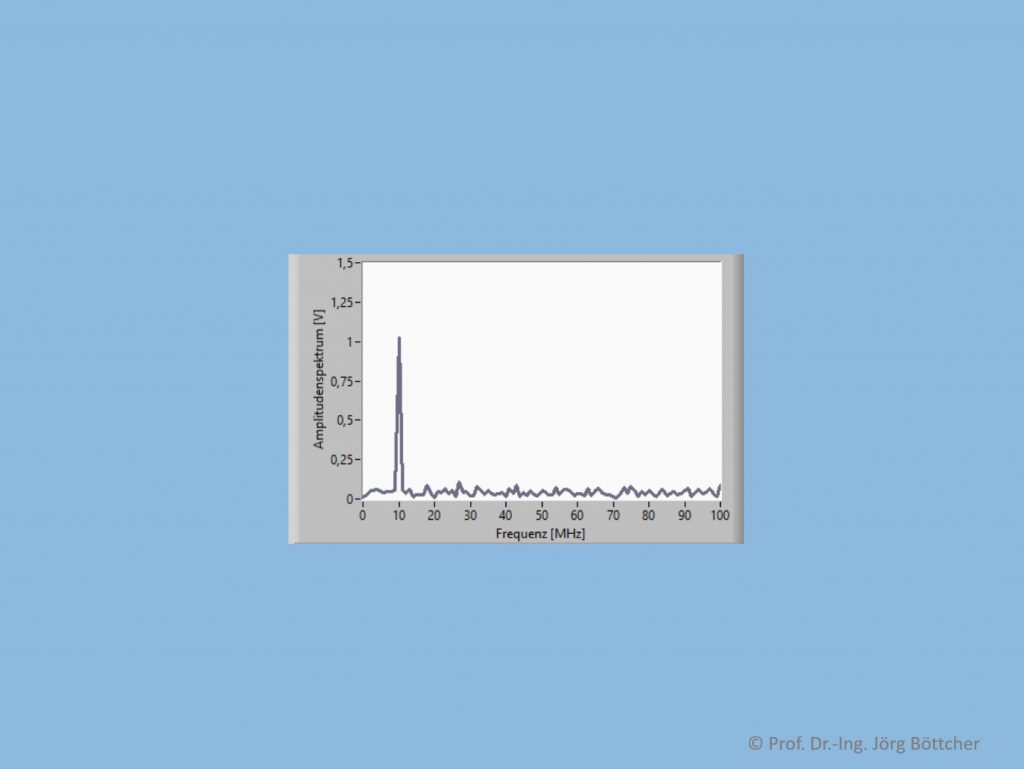
Spektrum des verrauschten Sinussignals
Auflösungsbandbreite, Sweep Time und Detektorfunktionen
Das Bandpassfilter im Spektrumanalysator lässt bei jedem Messvorgang lediglich einen schmalen, durch die Auflösungsbandbreite (RBW) definierten Frequenzbereich passieren. Über diesen ermittelt dann die nachfolgende Signalverarbeitung einen Pegelwert. Ein kompletter Sweep des Spektrumanalysators über die eingestellte Frequenzspanne besteht aus dem sequentiellen Verschieben des ursprünglichen Frequenzbereichs des Messsignals an dieser Filterglocke vorbei wie oben bereits aufgeführt.
Das Filter wirkt also wie eine an sich unerwünschte Glättung im Frequenzbereich. Der Glättungseffekt ist umso größer, je größer die RBW eingestellt wird. Dass man RBW insbesondere bei den ersten orientierenden Messungen dennoch eher größer einstellt, hängt damit zusammen, dass der Zeitbedarf für einen Sweep sehr stark (und überproportional) mit kleiner werdender RBW ansteigt.
Das nach Bandpassfilterung jeweils übrig bleibende Restsignal besteht zwar nur noch aus Spektralanteilen mit Frequenzen eng um die jeweilige Messfrequenz herum, stellt aber dennoch ein ganz normales Signal über der Zeit dar. Dieses wird nun mit sehr hoher Abtastrate abgetastet („gesampelt“). Die nachfolgende Signalverarbeitung ermittelt algorithmisch dann eine Art mittlerer Amplitudenwert. Dies sind die sog. Detektorfunktionen, von denen u.a. folgende meist einstellbar sind: Max Peak, Min Peak, Average, Effektivwert etc.
Kenndaten von Spektrumanalysatoren
Bei der Auswahl eines für bestimmte Messaufgaben geeigneten Spektrumanalysators sind u. a. die im Bild aufgeführten Kenndaten zu beachten:

Kenndaten von Spektrumanalysatoren
WENN SIE ES GENAUER WISSEN WOLLEN: