EIN
KOMPAKTER ÜBERBLICK

In diesem Überblick geht es um das Messen charakteristischer Kenngrößen von Signalen, die sich periodisch ändern, wir sprechen von „Wechselgrößen“. Die bekannteste Wechselgröße ist sicherlich die elektrische Wechselspannung von in Deutschland beispielsweise 230 V, wie sie aus der Steckdose „kommt“ und beim angeschlossenen Verbraucher zu einem Wechselstromfluss führt. Als weiteres Beispiel entsprechender Wechselsignale seien der periodische Druck- bzw. Temperaturverlauf im Zylinder eines laufenden Verbrennungsmotors genannt. Die bekannten englischen Abkürzungen speziell für Gleich- bzw. Wechselströme sind DC (Direct Current) und AC (Alternate Current).
Sinussignal mit Gleichanteil
Die mit Abstand häufigste Signalform einer Wechselgröße ist das Sinussignal. Dieses ist in Bild am Beispiel einer elektrischen Spannung skizziert. Im allgemeinen Fall schwingt das Sinussignal periodisch um einen sog. Gleichanteil (auch „Offset“ genannt) u0, der in vielen Fällen 0 ist:
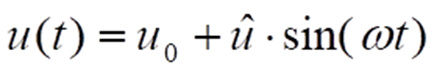
Weiterhin gelten bekanntermaßen:
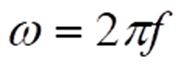
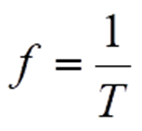
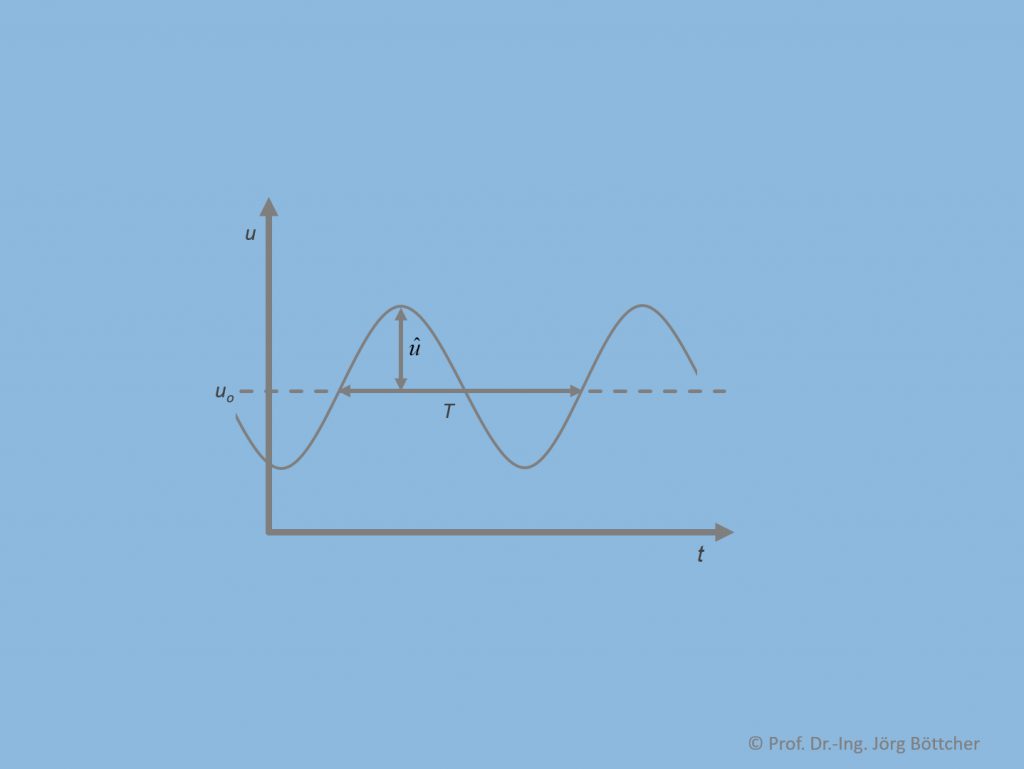
Sinussignal mit Gleichanteil
Kenngrößen
Als Kenngrößen derartiger periodischer Signale sind der (lineare) Mittelwert, der Gleichrichtwert und der Effektivwert eingeführt. Letzterer wird am häufigsten herangezogen. Er berechnet sich gemäß
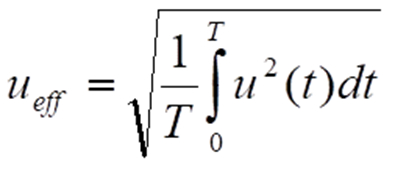
Die englische Abkürzung RMS (root mean square) umschreibt anschaulich die wichtigsten mathematischen Operationen hierbei. All diese Kenngrößen sind unabhängig von der Frequenz f des Signals. Zwischen ihnen sind Umrechenfaktoren definiert, die zu jeder speziellen Signalform einen konstanten Wert aufweisen (Scheitelfaktor, Formfaktor). Für ein gleichanteilsfreies Sinussignal ergibt obige Formel beispielsweise:
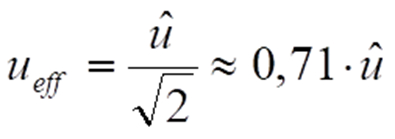
Ermittlung der Kenngrößen mit analoger Signalverarbeitung
Bei vielen Messsystemen für elektrische Wechselgrößen – primär betrifft es z.B. Multimeter und Messkarten/-module für PCs – werden derartige Kenngrößen durch eine analogelektronische Nachbildung der benötigten Rechenoperationen ermittelt. Nachfolgendes Bild zeigt das zugehörige Prinzip. Geräteintern wird dabei generell mit elektrischen Spannungssignalen gearbeitet. Zur Strommessung werden die Ströme hierzu zuerst in Spannungen umgewandelt. Ganz allgemein werden in der heutigen Messtechnik spätestens innerhalb der Messelektronik sämtliche elektrischen und nichtelektrischen Messgrößen fast ausschließlich in Spannungssignale umgewandelt, da diese einfach digitalisierbar sind.
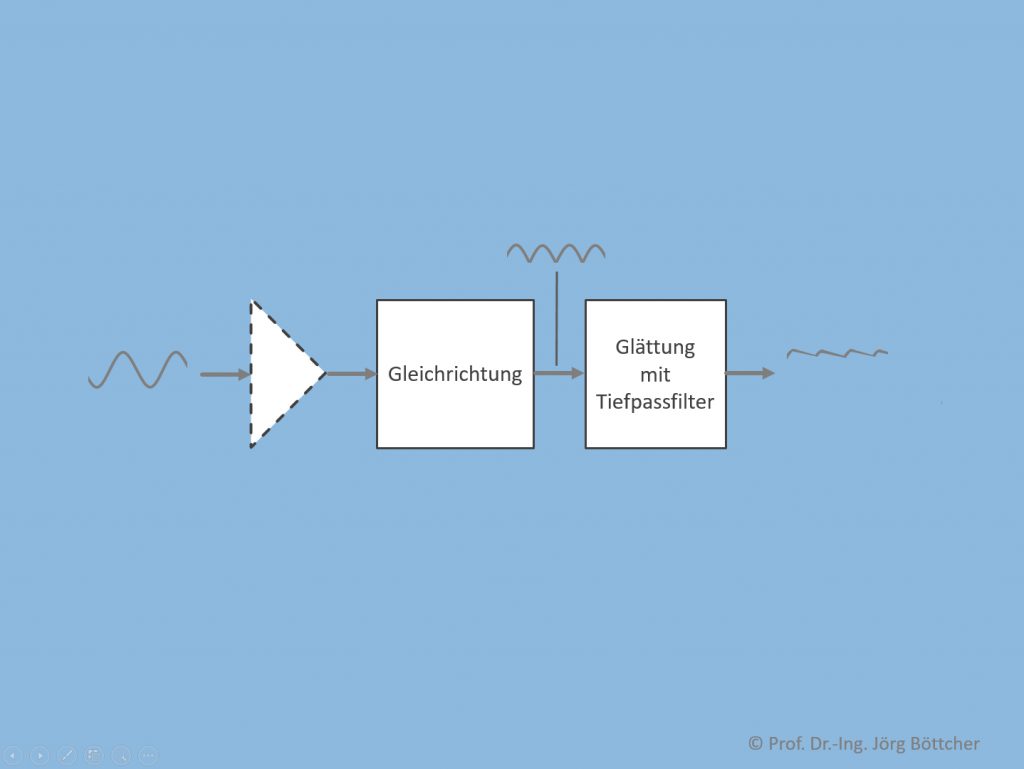
Bildung von Kenngrößen mit analoger Signalverarbeitung
Ermittlung der Kenngrößen mit digitaler Signalverarbeitung
Bei Messsystemen, die einen Rechner zur Steuerung, Auswertung und Visualisierung verwenden, werden mitunter direkt die Momentanwerte der Spannungssignale – auch hier werden letztlich alle Messgrößen auf Spannungssignale zurückgeführt – messtechnisch erfasst. Man spricht von der „Abtastung“ des Signals. Die Abtastung erfolgt in konstanten Zeitabständen TA. Auf Basis der abgespeicherten Momentanwerte können nun rein algorithmisch die Kenngrößen durch numerische Implementierung der entsprechenden Formeln berechnet werden.
Zur Berechnung des Effektivwerts gemäß obiger Formel ersetzen wir die Integralbildung durch die Aufsummierung vieler kleiner Rechteckflächen, jeweils mit der Breite TA und der Höhe des jeweiligen Abtastwertes uk:
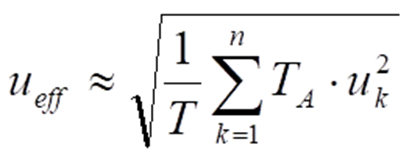
Frequenzgang analoger Komponenten
Werden Wechselsignale an messtechnische Komponenten wie Messkarten, Messmodule, Messgeräte etc. angeschaltet, so ist der sog. Frequenzgang dieser Komponenten zu beachten. Damit ist gemeint, dass eine analoge Schaltung (z.B. ein Verstärker) in ihrem Verhalten von der Frequenz des angeschalteten Signals abhängt. Zur Beschreibung geht man stets von Sinussignalen aus. Zwischen Aus- und Eingangsamplitude lässt sich ein von der Frequenz abhängiger Verstärkungsfaktor k(f) beobachten. Ganz typisch ist hierbei ein Verlauf, wie ihn das Bild zeigt.
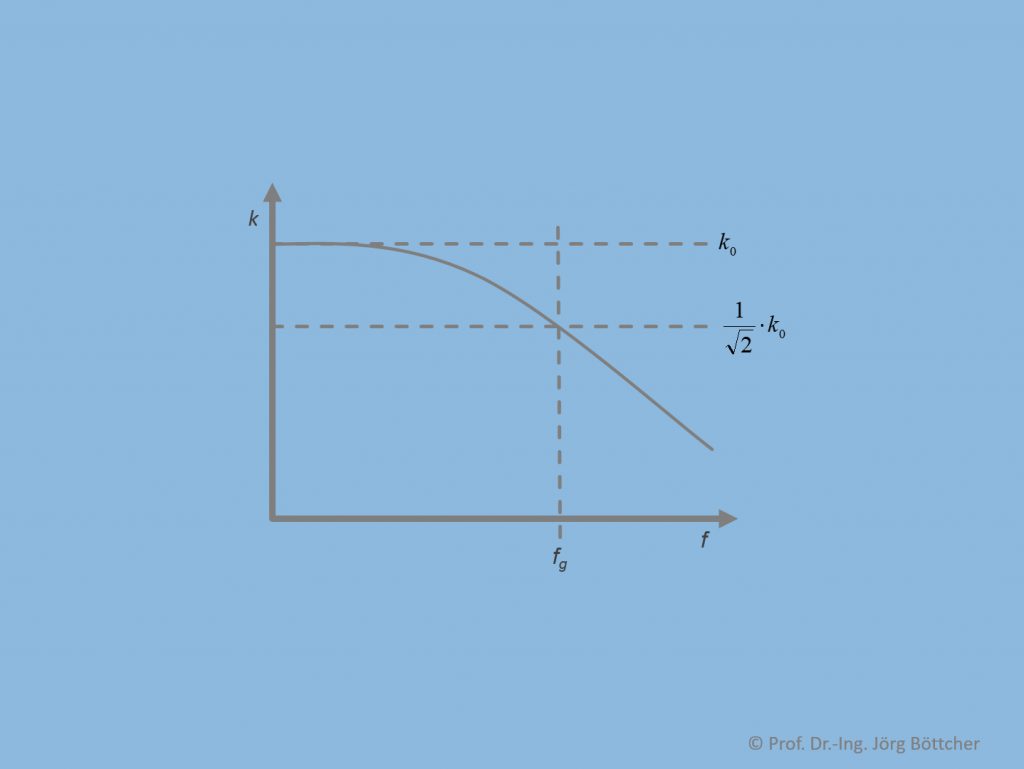
Typischer Frequenzgang eines Verstärkers
Bei nicht zu hohen Frequenzen entspricht der reale Verstärkungsfaktor weitgehend dem eingestellten k0, fällt jedoch mit zunehmender Frequenz dann ab. Man definiert hierbei eine sog. Grenzfrequenz fg, die einen Rückgang des Verstärkungsfaktors um exakt den Divisor Wurzel 2 kennzeichnet, was einem ca. -3 dB-Abfall entspricht. Man spricht auch von der „Bandbreite“ des Verstärkers und meint dann den nutzbaren Frequenzbereich von 0 bis zu dieser Grenzfrequenz.
Welchen Einfluss die Grenzfrequenz auf die Verstärkung periodischer Signalformen hat, wollen wir am Beispiel eines gleichanteilsfreien Rechtecksignals demonstrieren:
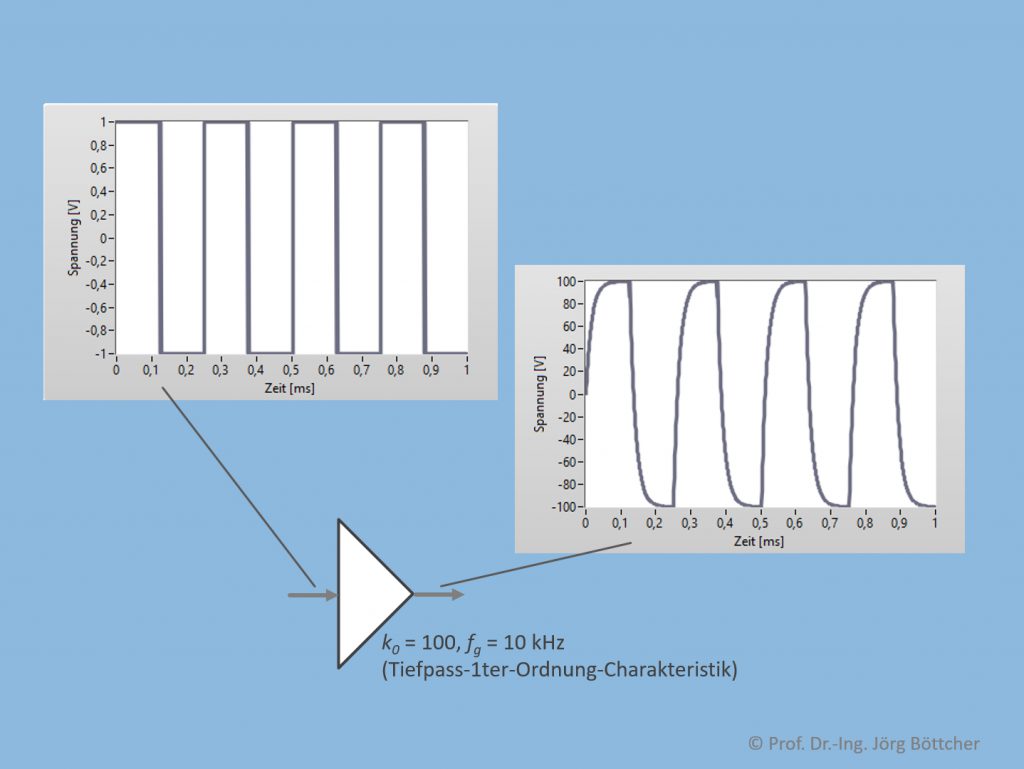
Signalverfälschung durch begrenzte Bandbreite
Die gemäß der spektralen Zusammensetzung eines Rechtecksignals enthaltenen Sinusanteile werden mit zunehmender Frequenz in steigendem Maße gedämpft, was zu einer deutlichen Signalverfälschung führt.
WENN SIE ES GENAUER WISSEN WOLLEN: