EIN
KOMPAKTER ÜBERBLICK

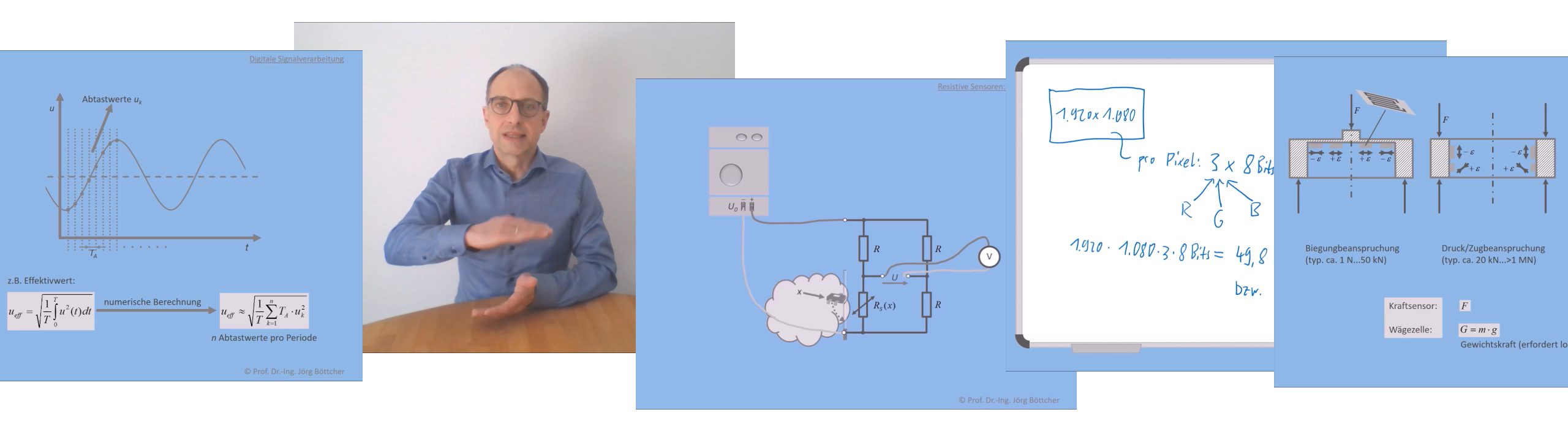
Die Messtechnik beschäftigt sich mit dem Messen von physikalischen, mitunter auch chemischen Größen. Sie dient damit z.B. dem Ingenieur, der Temperaturen und Drücke in einer Brennkammer analysiert. Oder der Waschmaschinensteuerung, die u. a. Temperatur, Feuchte, Stromverbrauch, Trommeldrehzahl und Trommelunwucht messtechnisch erfasst, um einen effizienten und energieschonenden Waschprozess zu erreichen.
Messen elektrischer und nichtelektrischer Größen
Messtechnische Lösungen basieren heute fast ausschließlich auf elektronischen Systemen. Elektronische Schaltungen können zunächst nur elektrische Größen wie Spannungen und Ströme oder auch elektrische Leistungen, ohmsche Widerstände, Kapazitäten, Induktivitäten etc. messen.
Für das Messen sämtlicher nichtelektrischer Größen werden in der Messtechnik Sensoren eingesetzt. Ein Sensor wandelt nach einem bestimmten physikalischen (oder chemischen) Funktionsprinzip die nichtelektrische Größe in ein elektrisches Signal um, das mit elektronischen Schaltungen weiterverarbeitet werden kann. Beispiele für über Sensoren erfassbare nichtelektrische Größen sind: Temperatur, Druck, Feuchte, Durchfluss, Weg, Winkel, Kraft, Druck, Beschleunigung, CO-Konzentration, Schalldruck etc.
Messgröße, Messsignal und Messwert
Wie das Bild am einfachen Beispiel einer Temperaturmessung zeigt, geht es in der Messtechnik stets darum, eine an einem bestimmten Ort herrschende „Messgröße“ mittels eines geeigneten Aufbaus in einen „Messwert“ überzuführen. Der Messwert kann uns wie im Bild durch ein Messgerät direkt angezeigt werden oder er kann nachfolgenden elektronischen Systemen zur Weiterverarbeitung in geeigneter Form zugeführt werden.
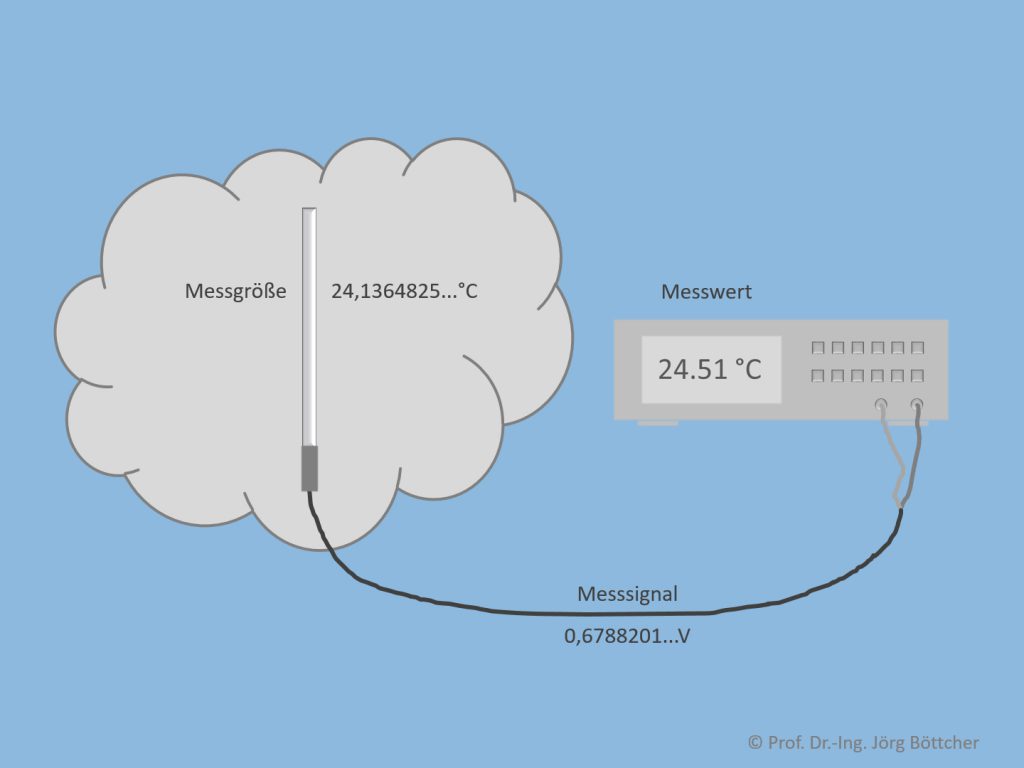
Messgröße, Messsignal und Messwert
Frühere Maßsysteme
Ein Messwert besteht aus einem Zahlenwert und einer zur Art der Messgröße passenden Einheit. In der Geschichte der Menschheit wurden in vielen Kulturen frühzeitig bereits Maßsysteme entwickelt, um für wichtige Größen des täglichen Lebens eine gemeinsame Basis zu schaffen. Darunter fallen vor allem Längen- und Gewichtsmaße. Erst mit der zunehmenden Durchdringung der Gesellschaften mit wissenschaftlichen Methoden, der Zunahme auch an weiteren interessierenden Messgrößen sowie letztlich der einsetzenden Industrialisierung wurden übergreifende Einheitensysteme etabliert. Ein Meilenstein war hier die Einführung des metrischen Maßsystems, welches das „Meter“ als zentrales Maß und die heute übliche dezimale Abstufung vorsah. Fast alle industrialisierten Staaten führten dieses System im 19. Jahrhundert ein. Am 8. August 1870 trat in Paris zum ersten Mal die Internationale Meterkonvention zusammen, in der diese ihre jeweils nationalen Regelungen zum metrischen Maßsystem harmonisierten. 1960 wurde von dieser schließlich das heute weltweit gebräuchliche Internationale Einheitensystem (Système International d‘Unités, abgekürzt SI) verabschiedet.
Das Internationale Einheitensystem
Das SI basiert auf der Erkenntnis, dass sich alle relevanten Messgrößen über physikalische Gesetze auf einige wenige, genauer gesagt sieben Basisgrößen zurückführen lassen. Zu diesen sieben Basisgrößen sind Basiseinheiten eindeutig definiert. Diese sind:
- m (Meter)
- kg (Kilogramm)
- s (Sekunde)
- A (Ampere)
- K (Kelvin)
- mol (Mol)
- cd (Candela)
Seit dem am 20. Mai 2019 abgehaltenen Weltmetrologietag werden die sieben Basiseinheiten über entsprechend reproduzierbare Experimente zurückgeführt auf sieben Naturkonstanten.
Das SI umfasst im Weiteren eine Aufzählung der von diesen sieben Basiseinheiten über physikalische Gesetzmäßigkeiten (oder auch nur Definitionen) abgeleiteten Einheiten. Ein Newton (N) beispielsweise definiert man über das bekannte gleichnamige Trägheitsgesetz
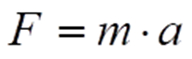
mit F Kraft (in N), m Masse (in kg) und a Beschleunigung (in m/s2) als 1 kgm/s2.
Neben den sieben Basiseinheiten und den abgeleiteten Einheiten definiert das SI noch zwei sog. ergänzende Einheiten, den Radiant (rad) und den Steradiant (sr), sowie Vorsätze, mit denen Vielfache bzw. Teile von SI-Einheiten in Kurzform angegeben werden können, von y (Yokto: 10-24) über die meist eher geläufigen wie d (Dezi: 10-1) oder k (Kilo 103) bis zu Y (Yotta: 1024).
Nicht-SI-Einheiten
Zusätzlich zu den offiziellen SI-Einheiten gibt es zahlreiche Einheiten, die international oder zumindest in einer größeren Region akzeptiert sind. Sie lassen sich i.d.R. auf entsprechende SI-Einheiten zurückführen. Beispiele sind das Grad Celsius °C als Temperatur in K plus 273,15 oder das (Winkel-)Grad ° als das π/180-fache von rad. Auch die zahlreichen historisch gewachsenen angelsächsischen Einheiten z.B. für Längen (wie mile, yard, foot, inch), Volumen (wie gallon), Masse (wie ounce, pound) etc. lassen sich in SI-Einheiten umrechnen.
Logarithmische Messwertangaben
Bei dieser ebenfalls im SI vorgesehenen Schreibweise eines Messwerts wird dieser stets auf einen definierten Referenzwert bezogen – also der Quotient gebildet – und danach logarithmiert. Der sich ergebende neue Wert trägt als Einheit das Bel (B) bzw. – auch dies wiederum die meist verwendete Variante – Dezibel (dB), also das Zehntel eines Bels. Im Falle einer elektrischen Leistung P wäre die übliche logarithmische Darstellung
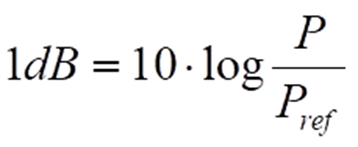
Die meisten anderen Größen werden in leicht abgewandelter Form – hier am Beispiel der elektrischen Spannung U – gemäß
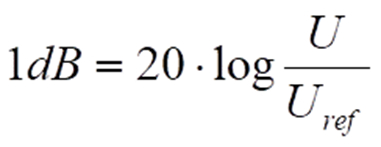
dargestellt. Die verbreitete Schreibweise von z.B. „dB(mW)“ bedeutet dabei einen Leistungspegel, bezogen auf 1 mW. 100 µW wären also – 10 dB(mW). Für Spannungspegel gilt entsprechendes. Die Angabe „dBm“ hingegen ist Spezialfall und bedeutet einen Spannungspegel bezogen auf ca. 0,224 V.
Prüfen, Kalibrieren und Eichen
Unter „prüfen“ versteht man in der Messtechnik wie auch generell im technischen Bereich das Untersuchen, ob ein Prüfgegenstand bestimmte Vorgaben erfüllt. Diese sind hierzu als Prüfbedingungen in angemessener Form spezifiziert.
Mitunter verfügen messtechnische Systeme über Möglichkeiten, die werksseitig im Rahmen des Herstellprozesses erzielbare Messgenauigkeit nachträglich zu erhöhen. Dies geschieht durch gezieltes Anschalten bekannter Referenzgrößen an den Messeingang anstelle der im eigentlichen Betrieb zu messenden Messgröße. Der Fachbegriff für diese Einstellmaßnahme ist „Kalibrieren“.
Nochmals einen anderen Sachverhalt beschreibt der Ausdruck „Eichen“. Unter diesem versteht man die Prüfung und Stempelung eines Messsystems nach gesetzlichen Eichvorschriften. Betroffen davon sind Messsysteme, die im gewerblichen Verkehr bzw. Handel verwendet werden.
Metrologische und normende Institutionen
Auf nationaler, europäischer und weltweiter Ebene existieren zahlreiche Institutionen, die sich jeweils um Fachthemen aus der Messtechnik bzw. mit Relevanz für diese kümmern.
In Deutschland ist dabei der wichtigste Vertreter die PTB (Physikalisch-technische Bundeanstalt). Außer für die Bauartzulassung eichpflichtiger Geräte ist sie kraft Gesetz u. a. auch zuständig für die Darstellung gesetzlicher Einheiten, die Entwicklung nationaler Normale, die Darstellung der gesetzlichen Zeit sowie die Prüfung der Normale entsprechend akkreditierter Kalibrierlabore. Weiterhin auch für die Messtechnik relevant sind DIN-Normen (Deutsche Institut für Normung). Als Beispiel sei die DIN 1319 genannt, welche den Titel „Grundlagen der Messtechnik“ trägt und u. a. wichtige Definitionen zu Fachausdrücken und zur Angabe von Messunsicherheiten beinhaltet. Auf deutscher Ebene noch zu nennen ist der Verband der Elektrotechnik Elektronik Informationstechnik e.V. (VDE), der entsprechende weitere Regelwerke veröffentlicht.
Auf internationaler Ebene sind u.a. relevant die Internationale Meterkonvention, die das internationale Einheitensystem (SI) verantwortet. Außerdem die OIML (Organisation Internationale de Métrologie Légale), die sich in erster Linie um die internationale Koordination des gesetzlichen Messwesens kümmert. Auf Normungsseite sind international zu nennen die ISO (International Organization for Standardization) sowie die IEC (International Electrotechnical Commission). Deren europäische Pendants sind das CEN (European Committee for Standardization) und das CENELEC (European Committee for Electrotechnical Standardization). Schließlich sei noch das IEEE (Institute of Electrical and Electronics Engineers) erwähnt, das ähnlich dem deutschen VDE zahlreiche Standards herausgegeben hat, die weltweit als de-facto-Norm beachtet werden.
WENN SIE ES GENAUER WISSEN WOLLEN: